Оглавление:
Асимптоты функции. Алгоритм полного исследования функции
Научимся разыскивать прямые, к которым в определенном смысле близок график функции. Такие прямые называются асимптотами.
a) Вертикальные асимптоты.
Пусть функция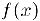 
определена в некотором интервале 
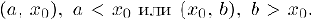. Если хотя бы один из односторонних пределов равен бесконечности, т. е.
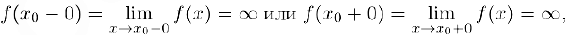
то прямая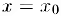 
называется вертикальной асимптотой функции .
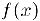b) Наклонные асимптоты.
Пусть функция 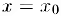определена на полуоси 
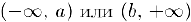. Прямая
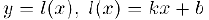
называется левосторонней (правосторонней) наклонной асимптотой функции 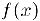, если существует предел
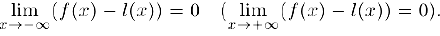
Если существует предел
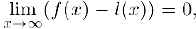
то наклонная асимптота является двусторонней.
Предположим, что наклонная асимптота существует. Найдем ее угловой коэффициент k и величину b. Так как
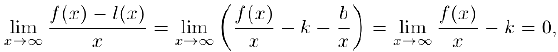
то
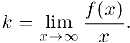
Тогда
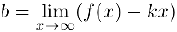
Верно, очевидно, и обратное, а именно, если существуют пределы (1) и (2). то существует также п предел
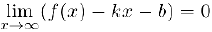
и, таким образом, прямая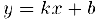 
— наклонная асимптота функции 
.
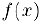Если хотя бы один из пределов (1) или (2) не существует или равен бесконечности, то функция не имеет наклонной асимптоты.
В качестве примера рассмотрим функцию
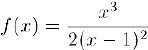
из предыдущего пункта. Для нее
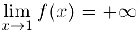
и, следовательно, прямая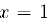 
— вертикальная асимптота данной функции. Выясним, обладает ли эта функция наклонной асимптотой. Для этого вычислим пределы (1) и (2).
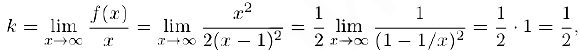
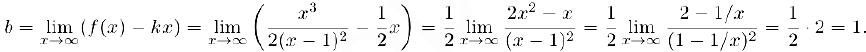
Таким образом, данная функция имеет двустороннюю наклонную асимптоту
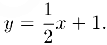
Сведем, наконец, воедино все наши изыскания этого параграфа и ( формулируем
Алгоритм исследования функции
1) Находим область определения функции, проверяем ее на четность (нечетность) и периодичность.
2) Исследуем функцию на непрерывность, находим се точки разрыва и асимптоты.
3) Определяем интервалы монотонности функции и ее точки экстремума.
4) Находим интервалы выпуклости (вогнутостчк) (функции и ее точки перегиба.
Результаты этого исследования дают нам достаточно полное геометрическое представление о поведении данной функции, которое мы можем реализовать в ее графике. Однако строить график «вручную» при наличии таких превосходных программ компьютерной математики, как Mathcmatica, Maple, Mathcad. было бы весьма архаично. Использование этих программ мы и рекомендуем для исследования функции и построения ее графика.
Завершим этот параграф построением графика функции
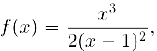
полное исследование которой мы провели в этом параграфе.
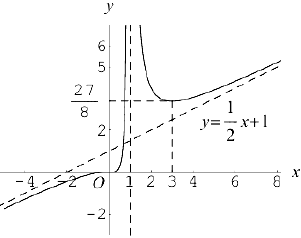
График функции построен в среде компьютерной алгебры Mathematica.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
