Алгоритм решения уравнений с разделяющимися переменными

Для решения уравнений с разделяющимися переменными целесообразно использовать следующий алгоритм:

1. Если в уравнении встречается 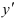, то представьте его как .
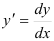2. Произведите разделение переменных (в одной части при 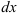соберите выражения, содержащие только переменную 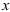; в другой части при 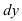соберите выражения, содержащие только переменную ).
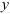3. Почленно проинтегрируйте обе части уравнения с разделёнными переменными.
4. Выпишите в ответе получившееся общее решение дифференциального уравнения.

Пример решения заказа контрольной работы №112.

Найдите решение дифференциального уравнения:

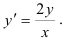
Решение:

Данное уравнение — дифференциальное уравнение с разделяющимися переменными. Представим

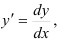
тогда

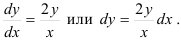
• Будем собирать множители с 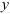в левой части, с 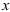— в правой:

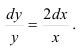
• Интегрируя обе части, получим:

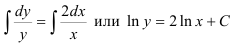
• общее решение.

Ответ:

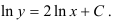
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:

Заказать контрольную работу по высшей математике

Другие похожие примеры возможно вам будут полезны:

Операция деления для комплексных чисел

Решение задачи Коши

Разложение функций в ряд Маклорена

Нахождение интервала сходимости для степенного ряда