Общее понятие об уравнениях
Алгебраической поверхностью (линией) называется множество, которое в какой-нибудь декартовой системе координат может быть задано уравнениями поверхности (1) и линии (2):
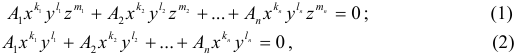
где все показатели степени — целые неотрицательные числа, а наибольшая из сумм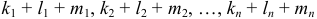 
для поверхности и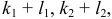 
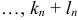для линии называется степенью уравнения, или порядком поверхности (линии).
Всякая неалгебраическая линия (поверхность) называется трансцендентной.
Теорема. Если поверхность (линия) в некоторой декартовой системе координат может быть задана уравнением вида (1) или (2), то и в любой другой декартовой системе координат она может быть задана уравнением того же вида, имеющим ту же степень. То есть порядок алгебраической линии (поверхности) является инвариантным.
Инвариантом называется всякая величина, не меняющаяся при изменении системы координат.
Представим себе, что линия — это траектория движущейся точки. В каждый момент времени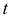 
нам известно положение точки, т.е. ее координаты относительно выбранной заранее системы координат. Тогда мы приходим к параметрическим уравнениям линии
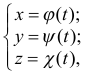
где 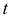— параметр.
По аналогии параметрические уравнения поверхности имеют вид
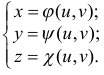
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Смешанное произведение трех векторов |
| Векторное и смешанное произведения в декартовых координатах |
| Различные виды уравнения прямой на плоскости |
| Определение угла между прямыми |
