Оглавление:


Аддитивность площади
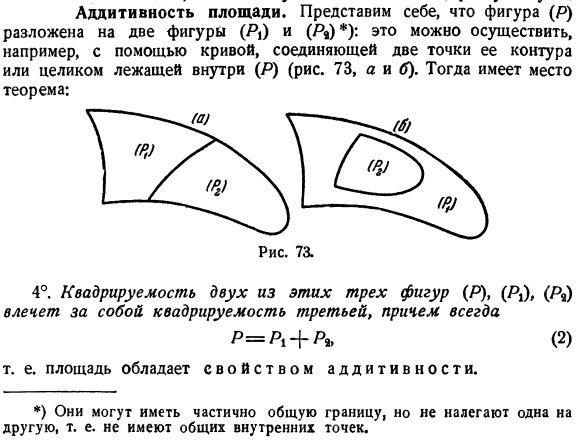
Аддитивность площади. Представьте, что фигура (P) разложена на 2 фигуры(P|) и(Pe)*): это можно сделать, например, с помощью кривой, соединяющей 2 точки контура, или кривой (P), которая полностью находится внутри(рис.73, a и b).Тогда справедлива следующая теорема. 4°.Из этих 3 фигур (P), (P.) # 2 ортогональность, с 3-й ортогональностью, всегда P = P1 + P *(2).
То есть область обладает свойствами аддитивности. Людмила Фирмаль
- Вы можете частично иметь общую границу, но не перекрывать друг друга. Утверждение об ортогональности следует непосредственно из условия 2°. остается только доказать равенство(2).Рассмотрим входящие и исходящие полигоны (Lx), (5.) и (L), (B9), соответствующие фигурам(P.) и (P9).
- Из полигонов (A, которые не перекрывают друг друга), (A) формируется полигональная область (A) области A = A1 + A9, которая полностью содержится в области (P).Полигонов(3) и (#А), площади (Б), которые могут быть продублированы и в районе б ^ ВХ + ва, содержащий область (р) состоят. В то же время есть Л1-|-Л§^Р^В^В-]-в9 и А —АВ ^ РХ—РВ ^.ВХ-\ Б%.
То есть, нет общих внутренних точек. Людмила Фирмаль
- Поскольку числа P и Px + ^ a входят между собой одинаково, и в дополнение к произвольно близким границам A1 + A9 и B1 + B9, эти числа при необходимости будут равны. В частности, это PX ^ P, поэтому часть фигуры будет иметь меньшую площадь, чем вся фигура.
Смотрите также:
Решение задач по математическому анализу
| Дополнительные члены приближенных формул. | Площадь как предел. |
| Определение понятия площади. | Выражение площади интегралом. |
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

