Непрерывность суммы степенного ряда

Оглавление:

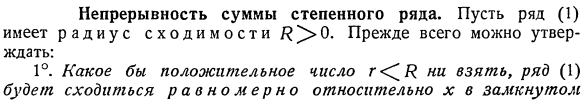
Непрерывность суммы степенного ряда

Непрерывность суммы степенного ряда. Предположим, что существует радиус сходимости β> 0 ряда (1).Прежде всего, можно констатировать следующее: 1°. это будет положительное число r ^ I. Кроме того, ряд (1) сходится равномерно относительно x в замкнутом состоянии Интервал [r, r]. на самом деле, поскольку это rKK, если x = r, то Ряд(1) будет сходиться абсолютно. То есть положительные ряды сходятся. 2 | А» | Р «= К | + / А1|-» + 1 ^ |-/-9 + … + | 2Н | Р + …(5） л * о в случае | l:| ^ r члены ряда(1) не превышают соответствующих членов этого ряда в абсолютном выражении, поэтому они играют роль основного ряда, и согласно критерию Вейерштрасса ряд (1) сходится равномерно к указанным значениям X.

Это привлекает внимание читателя к тому факту, что применение теоремы 1 было избегнуто в теории. Людмила Фирмаль

Число r может быть сколь угодно близко к R, но равномерная сходимость интервала(-R> R) не следует за доказанной: это также видно из примера прогрессии[n°264.5)]. Здесь, в результате теоремы 1, мы получаем n°266. 2°.Сумма степенных рядов (1) в интервале сходимости f (x) является непрерывной функцией от X. Между значениями x = x0, то есть-I и I>в интервале сходимости можно выбрать значение 0 ^ ^ C^. ЦДХ. Примените предыдущую теорему 1 к интервалу [r, r]и, принимая во внимание 1°, Установите непрерывность функции/(x) в этом interval. So, особенно о x = x0. [Фиксированная сходимость не может быть гарантирована интервал.

Непрерывность суммы степенных рядов может быть использована для доказательства теоремы о тождестве степенных рядов (аналогично аналогичной теореме для всего многочлена). 3°. 2 серии силы И 2 al ^Λ= a0 «Ч-»» • * * —&nxP 4• л * * * * И 2 bnxn = В0 -] б \ х -] б% х * … л = 0 В окрестности точки η= 0*, если сумма одинакова, то эти ряды идентичны. То есть каждый коэффициент равен каждой паре. #0 = ^ 0″ = О * = = = Г К = = П>••• Здесь имеется в виду не только окрестность по обе стороны от точки* = 0 (-5, 6), но и односторонняя окрестность вида (0, 5) или (* , 0]. Для идентификации. положить k = 0 * • • • • * * * * * * * * вы сразу увидите, что a0 = b0.

Эта теорема, устанавливающая единственность разложения функции в степенном ряду, впервые была указана Эйлером. Людмила Фирмаль

Отбросьте эти термины с обеих сторон письменного идентификатора и разделите на^(в этом случае вы должны рассмотреть Pi^ 0), чтобы получить новое удостоверение o.\ \ A%x { -… = б ьх { -… Кроме того, это делается в окрестности точки q; = 0, но сама эта точка исключается, поэтому нет права безоговорочно помещать x = 0 в это тождество. только непрерывность суммы обоих рядов при x = 0 позволяет заключить, что тождество сохраняется в исключенных точках, затем поставить-c = 0-отбросить эти члены, разделить на x ^ 0 и снова зависеть от непрерывности (просто), a ^ = b и так далее. Общее объяснение обосновывается методом математической индукции.

Пример непрерывной функции без производной.	Непрерывность на конце промежутка сходимости.
Промежуток сходимости степенного ряда.	Определение непрерывности функции в точке.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.