Оглавление:



Пример непрерывной функции без производной
Пример непрерывной функции без производной. Чтобы завершить этот раздел, мы используем ряд функций, чтобы показать пример неспецифической функции, которая не имеет конечной производной в любой точке. Первый пример такого рода принадлежит Вейерштрассу. Опубликовано в 1875 году); его функции определены ниже: И / (x) −2°n cos 6 ″ яхта、 Подробнее о L f Где 0 a 1, b-нечетные положительные целые числа^и ab > 1+^ -^. Ноль ноль Эта серия приводит к прогрессии сходимости 2L> [n°265; О 266, теорема 1], сходится равномерно, и его сумма является несогласованной функцией в любом месте x. благодаря кропотливым исследованиям Вейерштрасс смог показать, что по-прежнему нет конечной производной. Вот более простой пример N-D-R-VARDENA. Это в основном что-то построено на той же идее.
Таким образом, абсолютное значение разности между числом x и ближайшим целым числом обозначается через u0 (x). Людмила Фирмаль
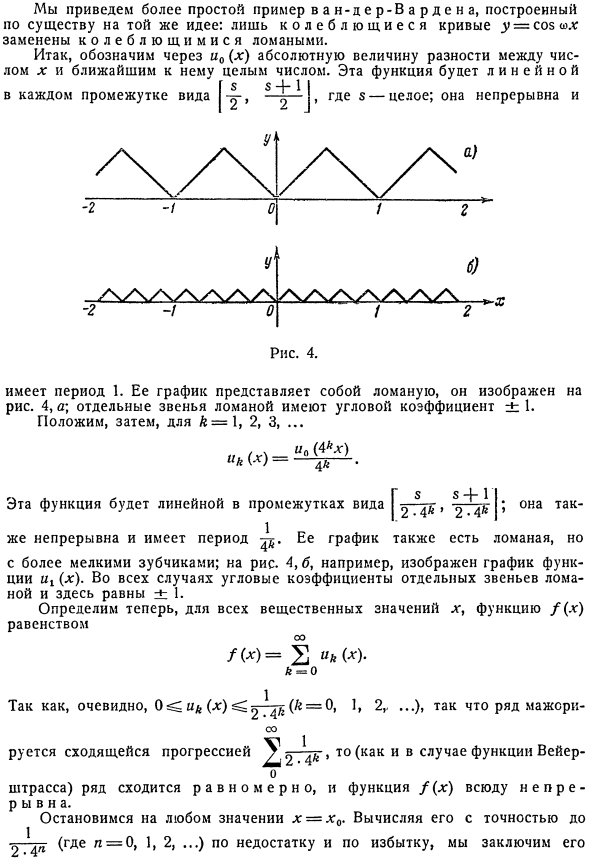
- Только кривая вибрации= sov заменяется ломаной кривой, которая вибрирует. Эта функция является линейной. [5 4-1 $ я ^ В каждом интервале формы$является integer. It непрерывна и、 11 К (Х)= (4 * AG) 4 * * Эта функция линейна по форме интервала 8 + П 2 ^ 1 ″ Она. Он имеет цикл I. Его график представляет собой пунктирную линию, которая показана на рисунке. 4 а; угловой коэффициент отдельных звеньев линии равен+ 1.Далее、&= 1、2、3、… Ее график был нарушен. На рисунке, например, 4.6 показан график функции u1 (x).во всех случаях угловой коэффициент отдельных звеньев линии равен±1.
- Теперь для всех действительных значений x определите функцию/(q)по уравнению. Ноль ноль / с*)= 2″ *(*)■ О, да. Очевидно, 0 u *(*) p (k = 0, 1, 2r …это хорошая идея.、 Ноль ноль Затем сходится(как в случае функции Бейера、 О Прямой) ряд сходится равномерно, и функция/(x) непрерывна везде. Рассмотрим произвольное значение x = x0. 2 ^по недостатку и избытку (i = 0, 1, 2,…Вычислить и заключить с точностью). Между числами в форме: 2.4 L 5 = 0 ^ 2•4L » Где$ l-это целое. Очевидно, замкнутое пространство = (^o. b 2,…) Вы можете видеть, что он вложен. Каждая из них имеет такую точку xm, что расстояние от точки x0 равно половине длины зазора. \ хп с x01 ^ л + | *、 увеличение n показывает переменную xn-x0.
Из этого следует, что функция x-x0 не имеет конечной производной, так как отношение приращения n-co не может быть конечным пределом. Людмила Фирмаль
- Создание инкрементного отношения Да. /(хп)/ (Хо)_ ый (хп)-Гонконге (ху) б = о Однако в случае k> n число является целым кратным периоду функции、()、 qi (*n)= u *(xA, соответствующий член ряда становится 0 и может быть omitted. in в случае k^ n функция u ^(q), Линейная в интервале u, становится линейной и включается в него. Интервал «»(*’■)С *(А’,> ^±1(п = 0,1,…, с.) хп х ^ Поэтому, в конце концов / (ХХ ^(Хо)= 2 (±、): Другими словами, это отношение равно четному целому нечетному n и нечетному целому четному n. У нас есть много веселья.
Смотрите также:
Решение задач по математическому анализу
| Почленное интегрирование рядов. | Промежуток сходимости степенного ряда. |
| Почленное дифференцирование рядов. | Непрерывность суммы степенного ряда. |
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

