Принцип сходимости

Оглавление:

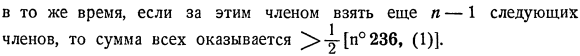
Принцип сходимости

Принцип сходимости. Направляясь к проблеме сходимости рядов, где члены могут иметь любой знак. знать [n°234] по определению задача сходимости ряда Ноль ноль 2 ап = ах+ -) -… + ап + ап + 1 + АП + Т +••• Л » 1 Тождественна задаче о существовании конечного предела последовательности частных сумм ^ 1 «• • * > К * ^ П + 1″•• * > ^ л + т»• * * о） restrictions.

Ранее был установлен принцип сходимости последовательности, который давал необходимые и достаточные общие условия для существования такой последовательности. Людмила Фирмаль

To перефразируя этот принцип применительно к последовательности(1), его можно сформулировать следующим образом: Для того чтобы ряд(A) сходился, каждому числу e> 0 соответствует такое число Ly, а в случае η> 0 этого неравенства достаточно. Я Ла + Вт-ЛП / = | АП + 1 + ап + * + * • • » («ап + т и Е(2） m = 1, 2, 3,… Он выполняется для*. (Где n \ m служит 2-м числом N ° 52.

Особенно если предположить, что ряд сходится на неравенстве(2), предполагая, что m = 1: I°l + 1 I e(для I> LO. Таким образом, он будет al + 1-0 или (то же самое) an-> 0 и вернется к необходимому условию n°236.5°.само по себе это еще не гарантирует сходимость ряда. Именно потому, что мы не исчерпали содержания вышеприведенных условий.

Это не зависит от n и может быть принято больше, чем n, без ущерба для общности. Людмила Фирмаль

Сколько? И еще возьмите их. Это хорошо объясняется гармоничным примером Строка 2, где общий термин ( = » ) имеет тенденцию быть 0’^’» Авторы этого условия-Больцано и коши-оба ссылались на проблему сходимости бесконечных рядов. В то же время, если вы используете другой n-1 из следующих терминов для этого термина, сумма всех будет]> y [n°236, (1)].

Признак Раабе.	Абсолютная сходимость.
Интегральный признак Маклорена-Коши.	Знакопеременные ряды.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.