Выражение длины дуги интегралом

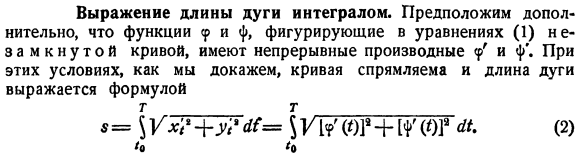
Выражение длины дуги интегралом

Выражение длины дуги интегралом. Кроме того, мы предполагаем, что функции φ и φ, возникающие в уравнении открытой кривой (1), имеют непрерывные производные p ’и / Γ.При этих условиях, как мы докажем, кривая корректируема, а длина дуги выражается формулой: (2） 4 = \ гг ’ 1 ′+ У1 ′ ае = [] / [?’(’)] * +Нет (01 * Я. / о Начните с точки из раздела в [интервал 7] Часть длины L1 = 11 + x-вершины соответствуют этим I значениям. Пунктирная линия, вписанная в дугу AMX AMX … Mn ^ x B, и (как обсуждалось выше) его длина s может быть определена как предел периметра пунктирной линии, когда X * = max стремится к нулю. Поставь y(1.)= x {, φ{1 {) = y {0 = 0, 1 n） Я = х,+ 1-х » Ду = ум-г, 0 = 0, 1,…я-1). Длина l-го звена с вписанной пунктирной линией выражается следующим образом: М, М1+, = г ВХ —1±г).

Достаточно найти, что разность p-a стремится к нулю, чтобы показать, что граница прямой p также стремится к тому же пределу. Людмила Фирмаль

• В духе применения функции Al / function(1) , Когда вы получаете формулу конечного приращения индивидуально, это выглядит так: / Их,= p 0,+ D () P 0.)=? ’(■*.) м» Al =φ0 / + u) −10)= » K OG) и{、 где значение M? Оба.(/И/(+!. Я ничего не знаю, кроме того, что он содержится между ними. лыл ^ = / [? ’ы] в + 1 +’ о? д) д、 Итак, для периметра всей полилинии получается следующая формула: Р = 2 / * Если вы замените m} 1 из 2-го члена под корневым символом преобразованным выражением «=2 / я? ’( * .)] ’+И]с. Я Очевидно, что это будет интегральная сумма для Интеграла(2). Если X * стремится к нулю, эта сумма содержит Интеграл) выше как a limitation. It Поэтому мы оцениваем эту разницу Если I P ’LH + [V»)]i 21■ I ’ S?+ А IV (.)]•Я ’、Я * ).

Подынтегральная функция непрерывна[n * 179, 1], поэтому ее существование не вызывает сомнений. Неравенство в начальных школах / ✓ » .»+»|/в * + 4 * Если применить к каждому из вышеперечисленных условий сумму индивидуально, то она будет выглядеть так I p °I 21Ф ’(т? V (х) IЛ«• Учитывая непрерывность функции (>’( * ), учитывая e}> 0 существует 8 0,|φ’ (/ ) (?Мне 11.-* 1 8 я не уверен. Возьмите все D*, [ & , затем u / m *-m * 1 8 и| [«„(Т?(’с*)| [e и | р-О | Е2 ^ = е(7—0). Я Это подтверждает наше утверждение. Если кривая задается явным уравнением декартовых координат у = F (Х) (Х ^ ^ Х ^ Х）、 Тогда мы получаем x в качестве параметра и этот частный случай из выражения (2). Х х * = 5 / Т + Г?4 * = 5 YT + ha? ** * (2а） ДГ#ха Наконец, для назначения полярной координатной кривой r = ёф) (0о6 0） Также сводится к параметрическому с использованием обычных выражений перехода x-ГСОЗ0 = ^ (0) Созо, у = гзш0 = ^(0) S! н 0.

• В этом случае x $ = Ge cos0-r s! н 0, ИБ = ы! н 0 + р cos0、 Так… (3） (26） ХВ *\ гг = г *\ г％ Второй 5 = 5/7 * + 75 г [г©)* +1В’^®] * л. Ноль ноль ) Это неравенство очевидно, если a = 0. если o ^: 0, он продолжается непосредственно из идентификатора П 4-Б -/ Л “+ Ь * = b + б Г-г 1 V Т Г#+ Г + я * + Р ’ 1 Разница в скобках заключается в том, что абсолютное значение коэффициента меньше 1. Замечания. Выражение (2) расширяется непосредственно в случае замкнутого curve. In в этом случае возьмите 2 между любыми 2 ′* 0 и Γ, разложите эту замкнутую кривую (1) из соответствующих точек M’(O на 2 открытые кривые AM и MV и примените уравнение типа (2) к каждой кривой отдельно： т. с {= АМ=], $ 9 = ЛДВ = $. / 0 в Добавьте эти результаты и для длины всего закрытого г 5 = $ 1 » b = 5• икс.

Пример 1) парабола: y = г х + ГУ топор = 5 = ом = п С вершиной 0 (π= 0) в качестве начала дуги, для любой точки M с абсциссой x: [1 * ух * + п> + ^ \ п(х + ух> + п)^ * Uhgrr + 4.1 а * ±УЕШЬ икс 2Р 2) циклоиды: х = а (*$1Н)> г-в(1-ой). Здесь(0 в 2k） Y x * й V(1-ой*) * un * * = 2a w Длина 1 ветви циклоиды по формуле (2)、 Второй C 2 ^ 12 * 8-2a I 8H ^ 11 = 4 Все I = 8a. О 3) спираль Архимеда: g = db. По уравнению (26), Если считать дугу от полюса O до любой точки M (соответствующей углу 6)、 Шесть 5 = ОЛ1 = а ^ / Т ^ 0 = | [р / Тгр ’+ 1П(П + / Т + С5)]. Г Подставляя 0= -, она становится формулой, формально аналогичной формуле для длины дуги параболы[см. 1)]. 4) эллипс: g4-tu = 1.

Таким образом, длина эллиптической дуги представлена эллиптическим интегралом 2-го класса. Людмила Фирмаль

• Из (г Однако удобнее взять эллипсоид в параметрической форме. г:= a8W1Yy = ВСО $ 1.Очевидно. Куда? г * Б * Существует численный эксцентриситет эллипса. Но… ЧХ? + У? = В а ° с°8 * 1 + б * ООН * * = в % («БР) в * * * = А В1-я * 8 в、 Если вычислить длину дуги эллипса от вершины малой оси до любой точки первого квадранта, то получим: [n * 174, см. Также n * 183].как показано, этот факт породил название»овал». В частности, 4-минутная (1) длина контура эллипса представлена полным эллиптическим интегралом*） Два У1-Б * 51p позволяют вести съемку быстро * я 1(-А * Е («). О 」 5 = 4а-е (*). Длина всего контура.

Смотрите также:

Решение задач по математическому анализу

Определение понятия длины дуги.	Переменная дуга, ее дифференциал.
Длина дуги. Леммы.	Длина дуги пространственной кривой.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.