Оглавление:

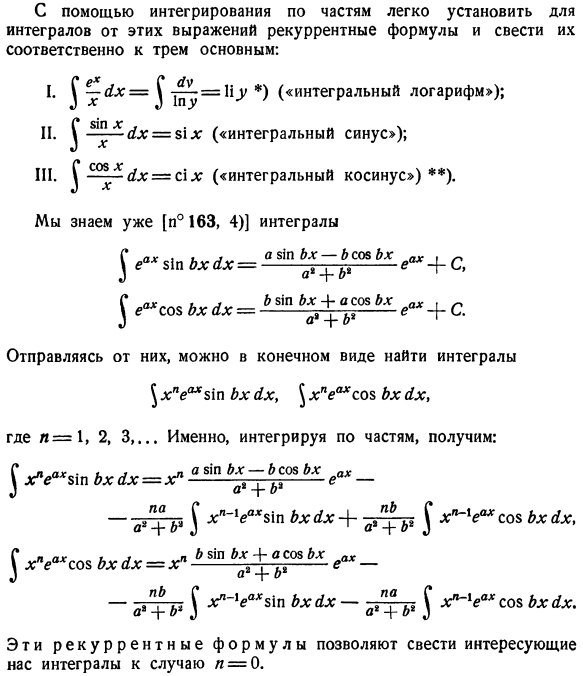

Интегрирование выражений, содержащих тригонометрические и показательную функции. Обзор других случаев
Интегрирование выражений, содержащих тригонометрические и показательную функции. Обзор других случаев. В разделе 163 мы уже упоминали, как можно интегрировать выражения форм. П (Х) е т™п (х) ж ВХ УГ, п ( * ), потому что ВХ&х> C1x потому что Х Шах.
Интеграция частей позволяет легко устанавливать рекурсивные выражения для интеграла этих выражений и сводить их к 3 основным выражениям. Людмила Фирмаль
- Где P-весь многочлен. Обратите внимание на дробное выражение(где n-натуральное число Он больше не интегрирован в своей окончательной форме. каждое. S ex s yoch I. V-c1x = ^ ^ = \ \ y.
- «Интегральный логарифм»); yh = b \ x («интегральный синус«); III. V-yx = c \ x («интегральный Косинус»)*). [n 163, 4)] мы уже знаем Интеграл $ Е * Ж ВХ топор = а 5 | н * * + ы、 5 а » потому что ВХ топором = + С. Исходя из них, Интеграл в конечном виде$ YY * * 51n bx xx,$ n ^ ^ cos bx 1x、 Где i = 1, 2, 3,…То есть, если вы интегрируете каждый из компонентов.
Эти рекуррентные формулы позволяют уменьшить интересующий Интеграл в случае π= 0. Людмила Фирмаль
- И zsh ВХ-Б потому что ВХ а * + б * Да. Шир. X выс. = хп 〜а * + б * ^ хп-1eax $ ВХ 1х\ ДГ ^ Г ^ Л ^ Е ^ потому что bxhx、 xpea * co5 bxAx = хп б 51nо * + б * -в ^ Тб $ У1 ’1 ^ $’ н bxlx ^ bxAx.
Смотрите также:
Решение задач по математическому анализу
| Интегрирование выражений вида R[х, sqrt(ax^2+bx+c)]. Подстановки Эйлера. | Эллиптические интегралы. Определения. |
| Интегрирование дифференциалов R(sinx,cosx). | Приведение к канонической форме. |
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

