Оглавление:


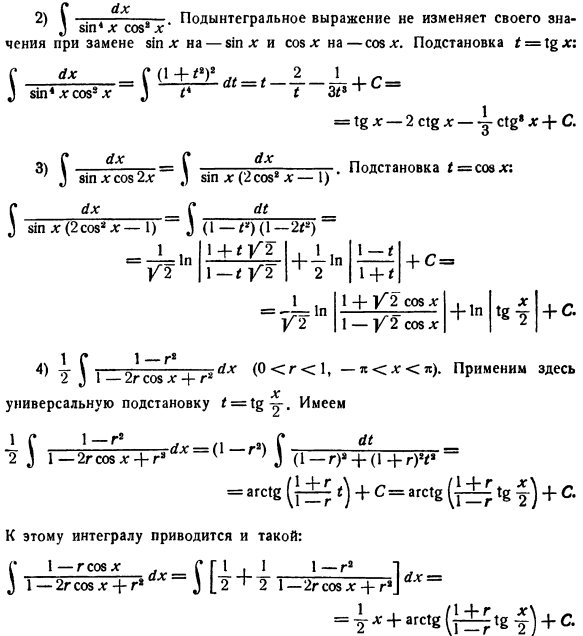

Интегрирование дифференциалов R(sinx,cosx)
Интегрирование дифференциалов R(sinx,cosx). $ в-ых х). Защита. Этот вид ферренала может быть рационализирован путем замещения. 81P X = + «Вт С08 ХХ-»» * Икс 2 1-я * −1 + 1 * * Два x = 2gs(2 *、 ых = В 1 + ** * Как это #(v1p х, С08 АГ) Два * 1 + * Я -* * \ ВТ Я + * / ’* + * * Р = * 2У (1С ^ ДГ ^ МК).Конечно. Так что интеграл типа Ноль) ^ Я(ь! Н С08 х) ух Она всегда принимается в окончательном виде. Для их представления, помимо функций, встречающихся при интегрировании рациональных производных, необходимы только тригонометрические функции. Ниже приведены случаи, когда цель может быть достигнута с помощью более простых замен. Во-первых, сделайте следующие основные замечания из области алгебры.
Вышеупомянутая подстановка, которая является универсальной для интеграла типа (1), может привести к сложным вычислениям. Людмила Фирмаль
- Например, если целая или дробная рациональная функция K (k, V) не изменяет своего значения при изменении любого знака аргумента, и К (Н.( ® ® ® ) = К (Н>>>®®®®®®)) » Тогда вы можете уменьшить его К(и в)= я, ( » , в)、 Включая только четные степени. И наоборот, если знак изменяется, функция K (k также изменяет знак, то есть Ж-и,= Жи, V)、 И затем… Я(у, М») = К (Н * * * >)•»; При применении это следует непосредственно из предыдущих замечаний 。 K(и V) Функция^I. Когда знак u изменяется, он меняет знак на K (n»x’).И затем… К(ЗС х, соѕ х)ух = ко (ЗС * х, потому что). = Ку-soz9, соѕ х) ysoh、 А рационализация достигается заменой {=Совх. I. аналогично, если K (u, V) изменяет знак, когда V изменяет знак、 К (51p позволяют вести съемку быстро, Соз х) ух = ко(ЗС, С059)С05ххх= = Со (31PDG, 1-51P9 х) (я 51p позволяют вести съемку быстро.
- Поэтому здесь подстановка I = z! N x подходит. III. наконец, если функция K (u, V) не изменяет своего значения, а u и Г-и «Р»)= К(У, в). В этом случае замените на-V、 {{У, В)= К {±В= Р «]. Из-за свойств функции K изменение знака u и V не изменяет отношение^、 «•(Т * -Г)= К *(т) *)• И » как мы знаем」 К ({Р -) = * Т(^ 4 Так… К (WX с, sozl)=/?? ’( * $ * , КО $% Х)=!$ ^ 8х,|+) е»х)> #(B1P х, Соз х)= у (*Е Х)’ Где: заменить(= 1 $ x ^ y [x, потому что ($ хху соѕ х) (1xk (^) и т. д Примечание. Например, вы можете поставить Я.«( В)= *〜(〜>■+ (〜» «„>(—П)+ и/? (м-в)+ {(U, в) Я 2.• Первое из этих выражений изменяет знак n, второе выражение изменяет знак V, а третье выражение сохраняет значение при изменении знака N V.
Каким бы ни было рациональное выражение k (и » V), всегда следует говорить, что оно может быть представлено в виде суммы 3 выражений определенного типа, которые мы рассмотрели выше. Людмила Фирмаль
- Примените подстановку = cos; e, 2-е-подстановку* = s1plg и, наконец, 3-е-подстановку 1 = X%.So, для вычисления интеграла типа(1) этих 3 перестановок достаточно. 1П $ х * поп * х С.,/, * * Я ^ страницы NN1 * в * Х、“ * х =] = б + с = —3-+ с * Три Пять Пример 1)^ НН * lgsoz * х-ых. Подынтегральное выражение меняет знак при замене СОС создать. Замены R = ЗТ *: О, да. 2) 1 подынтегральное выражение не меняет знака з! замените N dg на-81n d: и считайте значения при создании * on-sr. замените 1 = \% xx Г* * С(1±П1^ -, 2±+С3 БТ „dgcos8dg 3 С * я“ + с = х% х-2С \%х—ч 1г * х + с 。Замена* = соевого ХД !1П д; (2пк $ 8. *Я) З)С * х-г ’3 8ShLGS08 2 * 3 Г. ДГ. Г._ 3 PL x (2СО ® * L-1) зо -) (!’ №) / 2 ||-* / 2 +1р ^ 2 Один = ^=1Н 1-г + С: 1 + 1 + V ^ 2 cos d: + 1р + С 1 / 2 я1 л 1 г » 4) / 2gsoz + g8yh 0 g 1* * это не так. Пожалуйста, подавайте заявку отсюда икс Универсальная замена = 1 г 1-г,, _ Ач с А1 2 3 1-2 gsoslg + g> c(g 3 (1-g) +(1 + g) H *= АГС (Е)+ с = АГС 8 ′ 8 г)+ с Эта интеграция также приводит к: Г1 —гсобдгГГ1 i 1 1-г81 ^ 3 1-2gsozd:+ g * a 3 [2 ^ 2 T » Usovd.
Смотрите также:
Решение задач по математическому анализу
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

