Производные от сложных функций

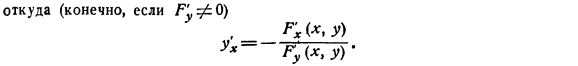
Производные от сложных функций

Производные от сложных функций. В форме применения полученной Формулы (1) мы будем иметь дело с проблемой различения сложных функций. Давайте сделаем функцию «=/(«Год> )> Определенная в области, каждая переменная x, y, r является функцией переменной I на определенном интервале. * * = Р (9.> = ’М0.* = Х (0Кроме того, когда я изменяю, я предполагаю, что точка (x, y, r) не превышает область Ж присвоение функции значений x, y и r дает сложную функцию. Α= /(p (0> ’ KO. X(0）предположим, что u имеет непрерывные частные производные по отношению к x, y и r и что существуют & u, y, u и x, y, y, r.По сути, переменной i на определенной добавочной Д1 дать координаты X, Y и R является соответствующее добавочное Д*, Ду, Д-г получаем функцию приращения Дн получат.

Тогда вы можете доказать существование производной комплексной функции и вычислить ее одновременно. Людмила Фирмаль

• Это можно сделать, выразив приращение функции в виде (1) (предполагая существование непрерывных частных производных ux, u, u）、 Ds = c’L. Ddydd llun -) и’. ДГ | а * дл:+ п * ду? * Генеральный директор、 Где a, {&, •(Дл, ду, ДГ ► O > * 0.Если мы разделим обе части равенства на Д1、 D и > ах, » Дю я * АГ ДХ, Ду ю, АГ М М = 11 * ’7 ^ +и y» 1С * +и * ’Л / + * * л7 + П * А7 + Т-тг Теперь повернем приращение Δ^к нулю. Поскольку функции, yотr ^ непрерывны (предполагая существование производных X/, Y \ и R}),*, у, будут, г стремятся к нулю, и поэтому a, p и 1 также стремятся к нулю. 。На пределе (3） Н \ =те * х \ + гг-й и* * Х). При допущениях мы можем видеть, что производные сложных функций действительно существуют. При использовании дифференциальной нотации уравнение (3) может быть записано следующим образом: (4 )） Ди-Ди-ых. Да ди ДГ Ш $ х * у Д1 * Д1 ДГ * дБ .

Вот случай, когда x, y и r зависят от нескольких переменных, а не от 1 переменной. Например в этом случае необходимо указать следующие параметры: dg = cp (, r»), y = qi V), r = x ((, r»). В дополнение к существованию и непрерывности частных производных функции f (x, y, r), здесь мы предполагаем существование производной функции X, y> 2 ^ ^ 1ЛV. Присвоение функций p, φ и χ функции/дает функцию 2 переменных I и V, что приводит к существованию частных производных u \и u ^и задаче вычисления. Однако этот случай существенно не отличается от уже изученного. Потому что, когда вы вычисляете частичную производную функции для 2 переменных, вы изменяете 1 из переменных, и все еще есть только одна функция для 1 variable.

• В этом случае Формула(3) не будет изменена, а Формулу (4) придется переписать в следующем виде: Ди di_ л*, д. du_ \ di_ ДГ… Д1 ДХ ’ Д1 ’делать’ Ы ’ ДГ ’ ДС ’ а ’ Образцы. 1) рассмотрим экспоненциальную функцию И-Сю. Если поставить ( * ), Y =φ (0, и дифференцировать только с производным правилом производной комплексной функции, то Лейбниц и Я. получена известная формула Бернулли. И\ = y * xY〜1 * x ^ + xULnx•y Ранее я установил его (в других обозначениях) с помощью искусственного приема[n * 85,(5)]. Выражение (3) аналогично выражению=в случае функции、 Однако еще раз подчеркнем различия между условиями, в которых были выведены эти формулы. Мы должны были предположить непрерывность между производными и # и u.

In в общем, Формулы (3) недостаточно. (для Q: + г> 0）、/（0、0）= 0 2) определить и задать функцию u = / ( * , y) . Как видно»этой функции имеет частный дифференциал во всех точках и не исключает» начальный (0 ″ 0」 /、（0,0 = 0、4（0,0-05 Обратите внимание, что в этот момент производные будут ломаться. Ввод новой переменной 1%put =дает вам комплекс function. By уравнение (3), производная от* = 0 этой функции имеет вид: в. ;год.°= ; Но с другой стороны, если вы на самом деле присваиваете значения x и y заданной функции » = / ( * , y) 9、 _ _ _ 1″ * + я * −2 Это также относится к 1-0. Если вы различаете непосредственно по отношению к, это также означает, что = 0 для любого значения. В этом случае можно видеть, что Формула (3) не применяется. А потом! 3)из уравнения = 1 переменная y определяется как функция X.

Достаточно было предположить существование производной в случае некоторых переменных, если они зависят от одной переменной. Людмила Фирмаль

• Дериват Ух = Б Х ы а * х * B1 * а * * г * г ± г * Х1(-а х）、 найдите эту производную, не решая уравнения Y. Если мы представим, что приведенная функция заменена уравнением y, то и последнее будет выполнено. Дифференцируя тождество результата относительно x (используя правила дифференцирования сложных функций) и、 Х2, Л3 + б> ух =°> Все равно откуда 4)В общем случае существует следующее уравнение: Р (Х, Y)= 0、 неразрешенный относительно y (/*здесь непрерывный с его производными).При определенных условиях(см. главу lX в Томе 2), используя это уравнение, мы можем думать, что переменная y определяется как функция X, Y, а также имеет производную (но не производную).

Смотрите также:

Решение задач по математическому анализу

Частные производные.	Полный дифференциал.
Полное приращение функции.	Инвариантность формы (первого) дифференциала.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.