Максимумы и минимумы; необходимые условия

Максимумы и минимумы; необходимые условия

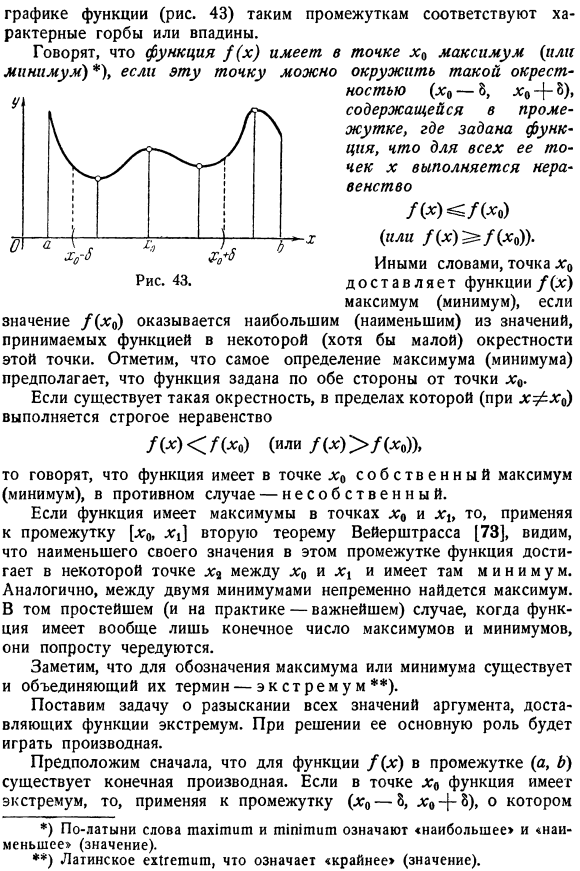
Максимумы и минимумы; необходимые условия. Если интервал [a, b]определен и последовательные функции f (x) не являются монотонными, то участок[A, b]интервала[a, b] имеет часть, в которой функция достигает внутреннего максимального или минимального значения. Между точками, а именно air. In на графике функции (рис. 43) такой интервал соответствует характерному горбу или впадине. Если функция может заключить эту точку в такую окрестность (0-8, x $ + 8), которая входит в заданный интервал, то функция x (x), как говорят, имеет самый большой (или самый маленький)в точке x0.

Если функция обычно имеет только максимальное и минимальное значение для конечного числа, они просто чередуются. Людмила Фирмаль

• Это точка x, неравенство / с * 0 ) < / (О) (или/(Х)> /(■»））、 говорят, что функция x6 имеет свое собственное максимальное (минимальное) значение. Иначе это будет неуместно. Если функция имеет максимальное значение в точках x0 и xi и применяет 2-ю теорему Вейерштрасса[73] к интервалу[x & xx], функция достигает минимального значения на этом интервале в точке x2 между x0 и xx, и мы видим, что там есть минимальное значение. Точно так же, есть, конечно, максимум между 2 minimums. In самый простой (на самом деле, самый важный) случай, Обратите внимание, что есть термины, которые объединяют их, чтобы указать максимальное или минимальное-экстремальное значение*).

• Возникает вопрос о нахождении всех значений аргументов, обеспечивающих экстремальные functionality. In решая ее, производные будут играть свою главную роль. Во-первых, предположим, что существует конечная производная для функции/(x) интервала (a, b). Если точка lgo функции имеет экстремумы, примените ее к интервалу (x $-8, -}»&«). * ) На латыни, Шах! Слова Tit и gttt означают самый большой «минимум» (значение). ** ) Латынь exPeshish. It означает «крайний» (значение). Мы заключаем, что это необходимое условие для экстремальных значений: теорема Ферма[n°100], f ’(xy)= 0, как описано выше. Экстремум следует искать только в точках, где производная равна нулю. Такая точка называется стационарной).

Однако не следует считать, что каждая стационарная точка обеспечивает функцию экстремальных значений. Людмила Фирмаль

• Условий, показанных сейчас, недостаточно. Например, в n°111.1 производная функции xr 3×8 исчезает при x = 0, но в этот момент функция не имеет extrema. It всегда будет увеличиваться. Таким образом, стационарная точка функции/ (), так сказать, Кажется только»сомнительной»по экстремумам и подлежит дальнейшему тестированию. Если расширить класс рассматриваемой функции, предположив, что в каждой точке нет конечных производных, то вероятность того, что экстремум падает на 1 из таких точек, не исключается. Поэтому необходимо также классифицировать и проверять его как»подозрительный»по экстремумам.

Смотрите также:

Решение задач по математическому анализу

Условие постоянства функции.	Максимумы и минимумы. Первое правило.
Условие монотонности функции.	Максимумы и минимумы. Второе правило.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.