Оглавление:


Условие монотонности функции
Условие монотонности функции. Теперь давайте найдем способ определить увеличение (уменьшение) самой функции на заданном интервале производной функции. Предположим, что функция теоремы f(x) определена в интервале 5C, внутри которого находится конечная производная f(x), и она непрерывна на обоих концах (если она принадлежит 3G). /(.x) быть 3?Если монотонно возрастать (убывать) в узком смысле, то условия достаточны. Д (х)> 0 0) в пределах 5р* Доказательство выполняется, если оно increases.
На этот раз указанные условия уже не являются полностью необходимыми. Людмила Фирмаль
- In в этом случае убедитесь, что указанные условия соблюдены. V и f(n / C * 0 из 3?Возьмите 2 значения) и примените формулу Лагранжа к функции f (x) в интервале[V, x. / СО— /(В)= / ’()(’- ’)(^ * *’)• А потом… / С * 0> / (б Функция f (x) строго возрастает. Утверждение теоремы справедливо даже в том случае, если, например, производная (x) исчезла в конечном числе точек внутри раздела 9.
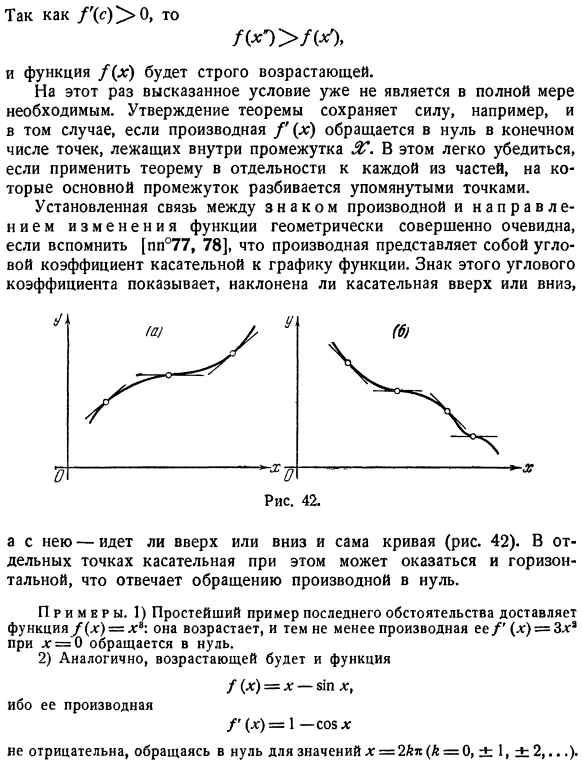
- Это может быть легко проверено, если теорема применяется индивидуально к каждой части, где главный интервал разделен в упомянутой точке. если вспомнить [pp°77, 78], то если вспомнить, что производная-это угловой коэффициент касательной к графу функции, то установленная связь между знаком производной и направлением изменения функции геометрически ясна. Кроме того, идет ли сама кривая вверх или вниз (рис.42).
Знак этого наклона указывает, идет ли касательная вверх или вниз. Людмила Фирмаль
- В определенных точках касательная линия также может быть выровнена, что соответствует исчезновению производной. Грунтовка. I) простейший пример ситуации последнего обеспечивается функцией f(x)= x: она растет, но ее производная f ’(x)= 3x *исчезает при q = 0. /(ЛГ)= х $ 1П *,/ ’(х)= 1-С05 * Для его производных 2) аналогично, функция увеличивается Не отрицательно, а значение x = 2kp(k= 0、±1、±2、…он исчезает в a).
Смотрите также:
Решение задач по математическому анализу
| Приближенные формулы. Примеры. | Максимумы и минимумы; необходимые условия. |
| Условие постоянства функции. | Максимумы и минимумы. Первое правило. |
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

