Оглавление:


Бесконечные производные
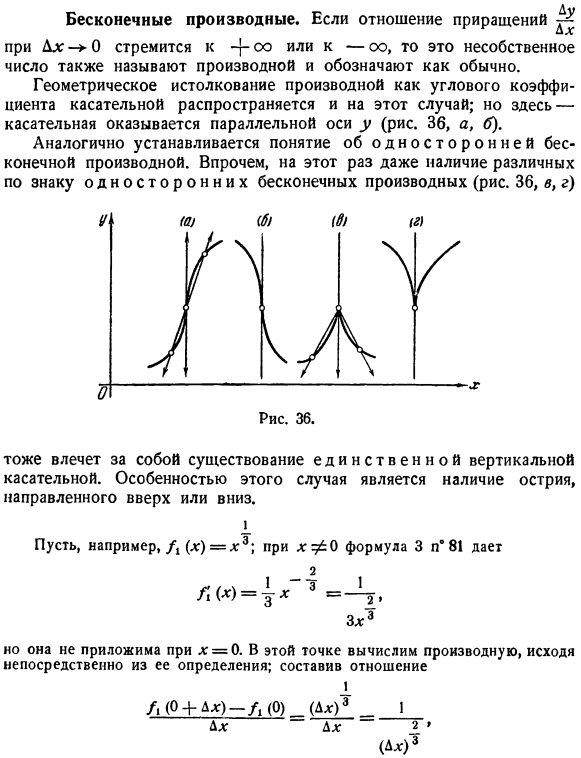
Бесконечные производные. Процент прироста^ Поскольку D * 0 имеет тенденцию быть {oo или k-oo, это неподходящее число также называется производной и отображается как обычно. В этом случае расширяется геометрическая интерпретация производной как углового коэффициента касательной. Но здесь касательные параллельны оси Y(рис. 36, а,<5).
Точно так же была установлена концепция односторонней бесконечной дифференциации. Людмила Фирмаль
- Однако на этот раз даже существование односторонней бесконечной производной с разными знаками (рис. 36, а, г) Он также сопровождается наличием единого вертикального касательного. Отличительной особенностью в данном случае является наличие фишек, направленных вверх или вниз.
- Например, если f4 (*)= x3; x> 0, то формула 3n * 81 имеет вид Один А (Х)= ^ Х 3 3 * 3 Завязывание отношений \ _ / , (0 + bx) -/, (0) (ад:) 3_1 2, 9 утра. (Л*) 3 Предел на Dx * 0 равен+ oo. Аналогично, мы подтверждаем Если функция fn (x)= xl равна* = 0, то производная слева равна-oo, а производная справа равна {co.
Однако это не относится к η.Этот пункт, вычислить производную непосредственно из ее определения. Людмила Фирмаль
- Используя расширение понятия производных, мы можем дополнить теорему n°80 обратной производной, указав, что производная$(y0) обратной функции существует и равна, если f(x0) равно нулю или±°°.. ±ОО Или ноль. Например, функция z * *из x =± это Поскольку производная равна cos ^ lb \ = 0, то для обратного, если a ^ c ^ b ^ / <y=: ±1, существует бесконечная производная (то есть -) oo).
Смотрите также:
Решение задач по математическому анализу
| Производная сложной функции. | Дальнейшие примеры особых случаев. |
| Односторонние производные. | Определение дифференциала. |
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

