Оглавление:




Ползучесть при изгибе
- Ползучесть при изгибе. Проанализируем некоторые простые задачи, которые решаются на основе теории стационарной полужидкости. Сначала рассмотрим изгиб стержня с поперечным сечением с двумя осями симметрии(рис. 298). Учитывая, что координатные оси TA’K выбраны, а изгибающий момент действует на плоскость UOG, как
показано на рисунке, x указывает скорость изменения кривизны нейтрального слоя. Затем приписывается гипотеза о сечении плоскости е=Ху. Рассмотрим закон полураспада в виде Затем е = ло.(197.1) Сечения изгибающий момент / «1 М = Дж абы ды=2 (сп)от J у ’ + » ды, Отчет (197.2) При этом предполагается,
что коэффициент ползучести при сжатии такой же, как и при растяжении. Формула Людмила Фирмаль
(197.1)сохраняется только в случае растяжения. Если L-целое и нечетное число, то эта формула справедлива для сжатия, а отрицательное напряжение соответствует отрицательной скорости деформации. Соответствующий для любого измерения индекса l и напряжения и обжатия правильный пар, следующим образом: § 197]ползучесть гнуть 443 Легко видеть, что такая запись всегда производит правильный символ. Давайте введем обозначение
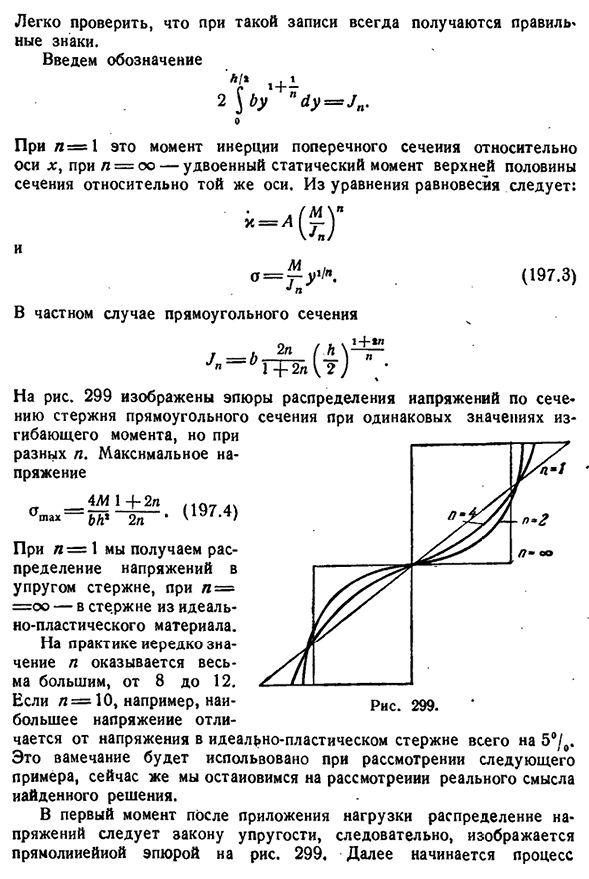
2 б у н д г=J и Н. Отчет При L=1 это момент инерции поперечного сечения относительно оси x, а при n=OO-удвоенный статический момент верхней половины поперечного сечения относительно той же оси. Из уравнения равновесия: И Дж » В некоторых случаях прямоугольного сечения (197.3) 1+2n2) J на фиг. 299 показана схема распределения напряжений по поперечному сечению стержня
- с прямоугольным поперечным сечением, с тем же значением изгибающего момента, но с другим п. В _4 2 и 14-2P(1 9 7 4)p-1 мы получаем распределение напряжений упругого стержня при L==o o-из STE. Полностью мой в пластиковом материале. На практике значение n часто бывает очень большим, от 8 до 12. Например, если l=10, то максимальное напряжение отличается от идеального напряжения пластикового стержня только на 5°/0. Это замечание используется в следующем примере, но теперь мы сосредоточимся на реальном значении решения. В первый момент после приложения нагрузки распределение напряжений подчиняется законам
упругости и, соответственно, представляется линейным участком рисунка. 299 затем начинается процесс 444 ползучести и длительной прочности[гл. XVIII Перераспределение напряжения ползучести. Теория установившейся ползучести ничего не может сказать об этом процессе; только после того, как достаточно долгое время было установлено, судить о силе отклика, заданной уравнением (197.3), строго говоря, материал, максимальное напряжение которого изменяется от начального значения, равного oM/bh1,
до заданного соответствующим уравнением (197.4). эквивалентное напряжение должно быть сопоставлено с долгосрочной кривой прочности, чтобы Людмила Фирмаль
учесть большее напряжение в процессе первого периода непрерывного перераспределения напряжения, установившееся напряжение ползучести составляет всего 3 ~ 4°/0. Можно определить отклонение луча, используя формулу скорости изменения кривизны. Возьмем, к примеру, балку длины I (рис. 300), R. нагруженный в середине сосредоточенной силой от-Р Крутящий момент L4=t R x; поскольку крутящий момент не зависит от времени, скорость изменения означает, Кривизна не имеет ничего общего со временем., Х=х-5=х/. ДХ? Здесь подставляя значение x через известный момент, находим следующее дифференциальное уравнение криволинейной оси: После интеграции、: программа В П+1 4-С(0. Угол наклона оси кривой должен быть равен нулю в центре луча X= / / 2. Отсюда функция времени C (t), вы [198]критическое время сжатого стержня Радж для производной отклонения равен: Четыреста сорок пять ДВ т(р \ н
[\п+1(я ДХ~Н+lk2jJ г\2Д Джей Начальное условие g>(0)=0 дано для повторной консолидации. Получаем: [P \ NF xn+2f I\»+1 1 -н+л (, 2jJ|п+2У; ХЈ- Определить максимальное отклонение pmav при X=/ / 2. Возьми: (1lp+Т Макс — {2JJ)н+2- По мере увеличения P криволинейная ось балки становится все более близкой к сломанной, что соответствует шарниру текучести детали, к которой приложена сила. Расчет ползучести стержней несимметричного поперечного сечения достаточно сложен, основная трудность заключается в обнаружении нейтральной оси поперечного сечения. В случае использования приближенной формулы это нейтральная ось, а если материал стержня полностью пластичен.
Смотрите также:
| Релаксация напряжений | Критическое время сжатого стержня |
| Длительная прочность при переменных нагрузках | Ползучесть и длительная прочность при сложном напряженном состоянии |

