Оглавление:




Уравнение трех моментов
- Три мгновенных уравнения. Чтобы рассчитать непрерывную длину балки, то есть балки, лежащей на двух или более опорах и не имеющей внутренних шарниров, условимся поддерживать число по порядку от самой левой опоры до самой левой опоры базовой системы. Рассмотрим наличие общего опорного числа i для
пролета I-1 и g. Let1{длина пролета. Чтобы обеспечить непрерывность касательной, пару моментов, которые нужно приложить к краю среза этой опоры, возьмем один из лишних неизвестных. Величина этого момента равна величине изгибающего момента неразрушенной балки. По — § 160] формула трех моментов 349
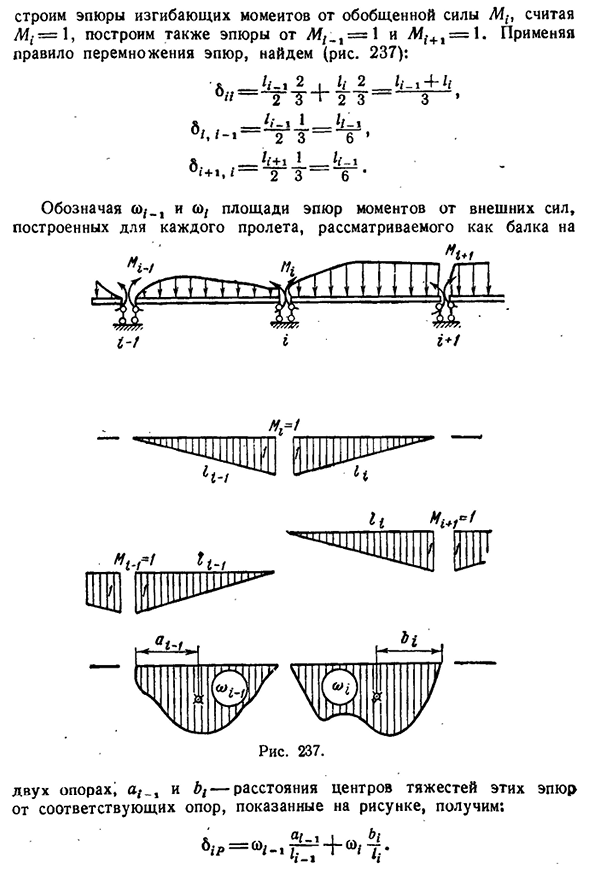
Мы строим изгибающий момент из обобщенной силы, считая L4;=1, мы также Людмила Фирмаль
строим из L4 / 1=1 и Aff+I=L. двести тридцать семь): ■Я_с-1 2|я, 2__1/14-ЖЖ А2 ″ з «2z паза з’ I _ lj+i1_ _ lj-1′+>. И2 3-6′ Т-Т Я+Ф т-т. — МТ-РФ ЛТ-я Две опоры^а, -.А bt-расстояние центра тяжести этих участков от соответствующей опоры, как показано на рисунке, получаем: 350 сопротивление материала общая теорема(гл. XIV Введение выражения 8ip в выражение (159.1) выглядит следующим образом: •(160.1) Это так называемые три момента уравнение. Если балка
имеет опору l, то опора n-2 является излишней, и уравнение(160.1) должно быть n-2 раза, последовательно предполагая 4=2,3.. .. .. л-1. В некоторых случаях, если все пролеты были загружены одинаковой длины и одинаковым образом, то можно указать общее решение системы(160.1). Поставить/,= / = const,. 6 4-диск; — ^|=А1 = Конст. Уравнение (160.1) принимает вид: 4-47I,-|-7I+1=-A (160.2) является линейным разностным уравнением. Для таких уравнений применим
- тот же метод, что и для линейных дифференциальных уравнений. Ищем частичное решение уравнения (160.2) в виде L4(. = константа. Подставляя гипотетическое решение в уравнение, легко увидеть, что эта константа равна—L / 6. Далее находим общее решение однородного уравнения. Вранье. Ми = ИЦ. Подставляя это выражение в выражение (160.2), предполагая L=0 и уменьшая C’-1, вы получаете следующее выражение, которое вызывает C: 1 4C-J-C=0. И так оно и есть. И 1 =-2+K_3, C1= — 2 -)<3. Таким образом, общее решение
уравнения (160.2) равно^C (y-z-2)’+Ct(-K Z- 2)’ — 4 • (160.3) рассмотрим балки, имеющие много пролетов, и нагрузите левый край крутящим моментом Mo. Значение опорного момента должно быть уменьшено от одной опоры к другой по смыслу задачи. Итак, в Формуле (160.3) необходимо принять Ct=0. Получаем: L^S D Z-2) 1’.§ 160] три мгновенных уравнения 351 Когда 1=0 2I1 — =2IO. Таким образом, необходимо сказать, что _C x=my,=M t (V3-2/=m a(-0,27/. Посчитаем некоторые основные моменты: M t=-0,27 2I0, 2I,=0, 073L40, 2ia=-0,0168 2I».. . Если число пролетов конечное и исходит из граничного условия, то оно может быть задано около i=0.
Получаем: LG4=C,+C1 — £ , Людмила Фирмаль
ЛГА=С(З-2)*+4-С1(-З-2)а-4. Если вы решите эти уравнения, вы найдете C и C. Как показано в следующем примере- существует постоянная I=k моментов MA и MK, которая равна k Примените уравнение к моменту, когда вы думаете, что луч закрыт, например, как показано на рисунке. 238, вместо уплотнения, продолжим балку влево и закрепим ее на двух опорах, что числа i=0 и i = −1, расстояние между ними равно 1_x. закроем это положим в нее и запишем выражение
трех моментов для i=0 / _a=0 и Af_j=O. получим: 2AV + Avenue=-6£4.. * 0 (160.4) В следующем промежутке уравнение трех моментов создается обычным способом.
Смотрите также:
| Графоаналитический способ вычислений интеграла перемещений | Жестко-пластическое тело |
| Расчет статически неопределимых систем по методу сил | Поверхности нагружения |

