Оглавление:

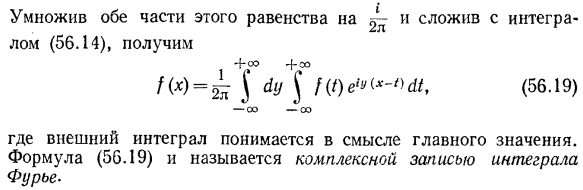

Комплексная запись интеграла Фурье
Комплексная запись интеграла Фурье. Вернемся к уравнению Фурье (56.14) и опишем в другой форме, используя понятие основного значения интеграла. Так как подынтегральная функция интеграла (56.16) имеет нечетное число y, то согласно сформулированному определению главного значения интеграла、 — ]- Х + ОО (56.18) В. П. ^ гг ^}(()$ ту (х-1) (ч = 0. 56.
Ввиду того, что сходимость к пределу является по а равномерной в окрестности любого значения переменной а, дифференцирование под знаком предела законно. Людмила Фирмаль
- Интегралы Фурье и преобразования Фурье 398. Если вы умножите обе стороны этого уравнения на^и добавите к интегралу (56.14), вы получите: + 00 + со НХ)= я | ю ^ /(/) ЕС (х — {) у,(56.19) — Ко-ко — Здесь Внешний Интеграл понимается в смысле главной ценности.
Выражение (56.19) называется комплексным представлением интеграла Фурье. Людмила Фирмаль
Смотрите также:
Решение задач по математическому анализу
| Различные виды записи формулы Фурье. | Преобразование Фурье. |
| Главное значение интеграла. | Интегралы Лапласа. |

