Классическое определение вероятности с примерами решения и образцами выполнения

Мы рассмотрим некоторые вероятностные пространства, объединенные интуитивным понятием симметрии или «равновероятности». В соответствии с тем, какое пространство элементарных исходов рассматривается -конечное или непрерывное, понятие «равновероятности» реализуется в двух схемах: классической и геометрической вероятности. Как всегда, право на жизнь вышеперечисленных схем определяется практикой. В различных учебниках приводятся результаты многочисленных статистических опытов, подтверждающих корректность понятия «равновероятность».

Классическая вероятность

Понятие классической вероятности мы рассмотрим сначала на примере нашей «палочки-выручалочки» — монеты. Предположим, что опыт состоит в однократном подбрасывании монеты. Как мы теперь знаем, пространство элементарных исходов 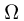содержит два элементарных исхода: 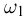— выпадение «герба» и 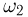— выпадение «цифры», а 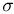-алгебра насчитывает 4 события: 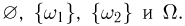Ясно, что обычная монета обладает свойством симметрии, так как у нас нет оснований предпочесть «герб» «цифре», т.е. элементарный исход 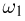элементарному исходу 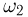Поэтому естественно сопоставить обоим элементарным исходам одинаковую вероятность 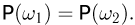Так как согласно аксиоме сложения 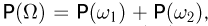а в силу аксиомы нормированности 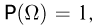то получаем 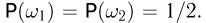Таким образом, каждому из четырех имеющихся в 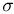-алгебре 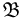событий мы ставим в соответствие вероятности: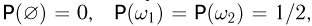

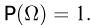
Перейдем теперь к общему случаю. Пусть пространство элементарных исходов 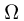состоит из конечного числа n равнозначных исходов 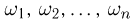(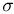-алгебра событий содержит 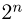событий). Тогда каждому элементарному исходу 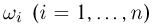поставим в соответствие одну и ту же вероятность 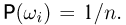Ясно, что в силу аксиомы сложения для определения вероятности любого события А необходимо подсчитать число m элементарных исходов 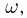содержащихся в А, и затем положить

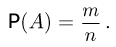
Таким образом, в классической схеме вероятность любого события А определяется как отношение числа т благоприятных для события А элементарных исходов к общему числу элементарных исходов п.

Пример:

Определим вероятность выпадения на игральной кости четного числа очков (событие А). В этом случае общее число элементарных исходов n= 6 (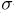-алгебра 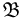состоит из 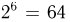событий), а число благоприятных исходов m= 3 (выпадение«двойки», «четверки» и «шестерки»). Искомая вероятность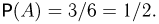

Пример:

Производится трехкратное подбрасывание монеты. Определим вероятность события А, заключающегося в выпадении «герба» хотя бы один раз. Выпишем все элементарные исходы:

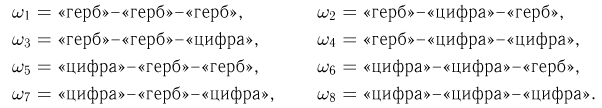
Всего имеем n= 8 элементарных исходов (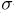-алгебра 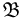состоит из 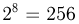событий). Благоприятными из них для события А являются m= 7 исходов: 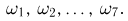Значит,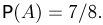

Вероятность Р(A) можно подсчитать и другим способом. Дополнительным к А будет событие 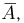заключающееся в невыпадении ни одного «герба». Событие 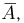состоит только из одного элементарного исхода 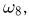поэтому 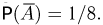Переходя снова к событию А, имеем 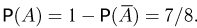Отметим, что привлечение дополнительного события позволяет иногда существенно упростить численный подсчет вероятности.

Пример:

Найдем вероятность того, что при бросании двух игральных костей в сумме выпадает не менее четырех очков (событие А). Поскольку при бросании двух игральных костей может выпасть от 2 до 12 очков, а рассматриваемое событие А состоит в выпадении 4, 5, …,12 очков, то удобно перейти к дополнительному событию 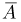— выпадению двух или трех очков. Пространство элементарных исходов состоит из 36 исходов — пар (1,1), (1,2), (2,1), (1,3) и т.д. (заметим, что пары (1,2) и (2,1) представляют собой разные элементарные исходы, поскольку выпадение одного очка на первой кости и двух на второй — не то же самое, что двух очков _на первой кости и одного очка на второй). Благоприятными для события 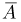будут элементарные исходы (1,1), (1,2) и (2,1). Значит, 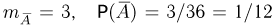и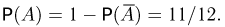

Пример:

Из колоды в 36 игральных карт наудачу выбирается одна. Определим вероятность того, что она окажется тузом (событие А). Из колоды мы можем выбрать любую из 36 карт (n = 36). Тузов в колоде 4 (m= 4). Таким образом,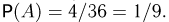

Элементы комбинаторики в теории вероятностей

Примеры, рассмотренные в предыдущем параграфе, имели ту характерную особенность, что для них нетрудно было подсчитать как общее число элементарных исходов, так и число исходов, благоприятных для данного события. Однако именно этот подсчет и представляет наибольшую трудность при решении более сложных задач на классическую вероятность. Для того чтобы иметь некоторые стандартные приемы при расчетах по схеме классической вероятности, приведем основную формулу комбинаторики и рассмотрим понятия перестановки, размещения и сочетания.

Пусть имеется k групп элементов, причем i-я группа состоит из 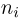элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением

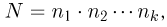
называемым основной формулой комбинаторики.

Для доказательства этой формулы рассмотрим сначала случай k= 2 и перенумеруем все элементы первой группы числами от 1 до 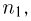а второй — от 1 до 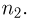Тогда каждый возможный способ выбора двух элементов отождествим с парой чисел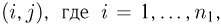

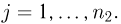
Очевидно, что таких пар 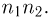Для окончания доказательства достаточно воспользоваться методом математической индукции. Так, для k= 3 всевозможные способы выбора трех элементов можно отождествить с тройками 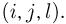Поскольку первые два элемента можно выбрать 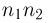способами, то все три элемента можно выбрать 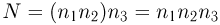способами.

В том случае, когда все группы состоят из одинакового числа элементов, т.е. 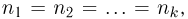можно считать, что каждый раз выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно 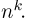Такой способ выбора носит название выборки с возвращением.

Перестановкой из п элементов называется любой упорядоченный набор этих элементов. Так, всевозможными перестановками чисел 1, 2, 3 являются: (1,2,3), (1,3,2), (2, 1,3), (2,3, 1), (3, 1,2) и (3,2, 1). Для определения числа различных перестановок из n элементов, которое мы будем обозначать через 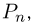заметим, что на первом месте перестановки может стоять любой из n элементов, на втором — любой из n-1 оставшихся, на третьем — любой из остальных n- 2 и т.д. В силу основной формулы комбинаторики (в данном случае мы имеем n групп элементов размеров 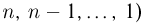получаем

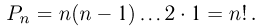
Размещением из n элементов по m называется любой упорядоченный набор из m различных элементов, выбранных из общей совокупности в п элементов. Выпишем для примера все размещения из четырех чисел 1, 2, 3, 4 по два: (1,2), (1,3), (1,4), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3). Число размещений 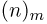(используется также запись 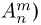подсчитывается точно так же, как и число перестановок: на первом месте может находиться любой из n элементов, на втором — любой из n-1 оставшихся,…, на m-м месте — любой из 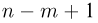элементов. Снова воспользовавшись основной формулой комбинаторики (выбор осуществляется из групп размеров 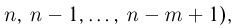имеем

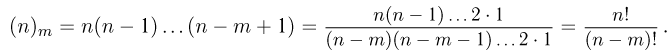
Заметим, что способ выбора, приводящий к перестановкам и размещениям, носит название выборки без возвращения.

Сочетанием из n элементов по m называется любой неупорядоченный набор из m различных элементов, выбранных из общей совокупности в n элементов. Сочетаниями из четырех чисел 1, 2, 3, 4 по два являются: (1,2), (1,3), (1,4), (2,3), (2,4) и (3,4). Для определения числа сочетаний 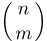(употребляется также запись 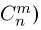заметим, что сочетание от размещения отличается только тем, что входящие в него элементы неупорядочены. Но, как мы знаем, m элементов можно упорядочить m! способами. Значит, каждое сочетание соответствует m! размещениям. Поэтому 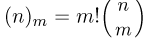или

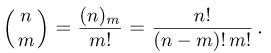
Вооружившись знанием формул для чисел перестановок, размещений и сочетаний, продолжим рассмотрение задач на классическую вероятность.

Пример:

На четырех карточках написаны буквы в, л, к и о. Карточки перемешиваются и выкладываются в ряд. Найдем вероятность того, что образовавшееся слово будет «волк» (событие А). В соответствии с комбинаторными принципами для определения общего числа элементарных исходов нужно подсчитать число упорядоченных наборов из четырех букв. Мы имеем дело с числом перестановок, поэтому число элементарных исходов 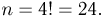Слово «волк» образует только одна перестановка, т. е. число благоприятных для события А элементарных исходов m= 1. Поэтому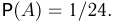

Пример:

Из колоды в 36 игральных карт вынимаются наудачу 3 карты. Найдем вероятность того, что все эти 3 карты будут одной масти (событие А). Для большей наглядности приведем два решения.

В первом решении будем предполагать, что выбор производится последовательно по одной карте и нужно учитывать его порядок. Тогда результат выбора отождествим с размещением из 36 карт по 3, и общее число элементарных исходов 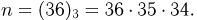Для подсчета общего числа благоприятных исходов предположим сначала, что мы последовательно вынимаем карты пиковой масти. Поскольку «пик» в колоде 9, то число способов, которыми мы можем последовательно вынуть 3 карты пиковой масти, равно числу размещений из 9 карт по 3, т. е. 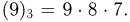Но благоприятными для нас будут также такие ситуации, при которых мы вынимаем 3 «трефы», 3 «бубны», 3 «червы». Поэтому для определения общего числа благоприятных исходов нужно число размещений из 9 по 3 умножить на 4: 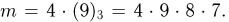Значит,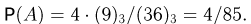

Во втором решении мы не будем учитывать порядок выбора карт. Тогда общее число элементарных исходов определяется уже как число сочетаний из 36 карт по 3, т. е. 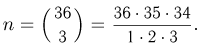Однако и при подсчете числа благоприятных исходов мы должны помнить, что порядок выбора несуществен, т. е. 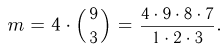Нетрудно видеть, что окончательное значение Р(A) будет тем же самым, что и в первом решении. Рекомендуем любознательному читателю еще раз разобрать этот пример и объяснить, почему в обоих случаях получился один и тот же ответ.

В заключение этого параграфа мы рассмотрим некоторые наиболее часто встречающиеся в физической практике задачи о распределении частиц по ячейкам.

Гипергеометрическое распределение

Предположим, что имеется 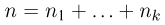различных частиц, причем из них 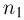частиц первого типа, 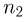— второго типа…, 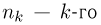типа. Случайным образом из этих n частиц выбирается 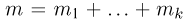частиц. Найдем вероятность того, что среди выбранных окажется ровно 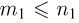частиц первого типа, 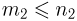— второго типа…, 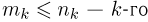типа (событие А). Поскольку порядок выбора несуществен, то при определении общего числа исходов и числа благоприятных исходов мы должны пользоваться числом сочетаний. Общее число элементарных исходов есть число сочетаний из n частиц по 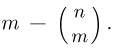Далее, 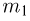частиц первого типа мы можем выбрать 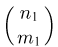способами, 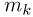частиц второго k-типа 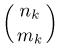способами. При этом любой способ выбора частиц определенного типа комбинирует с любыми способами выбора частиц остальных типов и, значит, число благоприятных событию А исходов равно 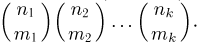По-этому

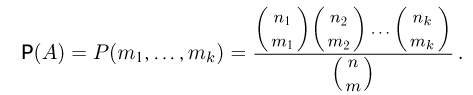
Определенные последней формулой вероятности 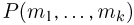носят название гипергеометрического распределения.

Пример:

Найдем вероятность того, что в «Спортлото 6 из 49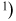 будет угадано 3 номера (событие 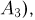4 номера 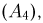5 номеров 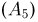и 6 номеров 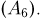Мы имеем дело с гипергеометрическим распределением, в котором n= 49,

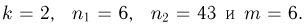Для события 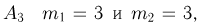для события 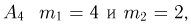для события 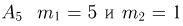и, наконец, для события 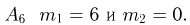Поэтому

Статистика Бозе-Эйнштейна

Предположим, что п неразличимых частиц распределяются по m ячейкам. Различными считаются распределения частиц по ячейкам, отличающиеся только числом попавших в каждую ячейку частиц. Такое распределение носит в физике название статистики Бозе-Эйнштейна. Найдем общее число различных размещений в статистике Бозе-Эйнштейна (число элементарных исходов). Для этого рассмотрим последовательность из 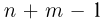элементов (рис. 1) и выберем из них m— 1 «черный» элемент. Если

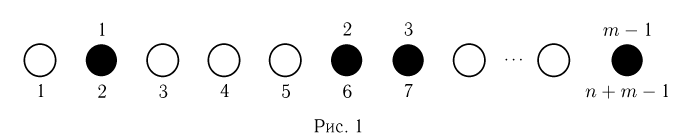
считать «белый» элемент частицей, а «черный» — перегородкой, то, как нетрудно видеть, существует взаимно однозначное соответствие между способами выбора m-1 «черного» элемента и размещениями частиц в статистике Бозе-Эйнштейна. Так, на приведенном рисунке в первую ячейку попала одна частица, во вторую — три, третья оказалась пустой,…, последняя, m-я ячейка также оказалась пустой. Поэтому общее число размещений равно 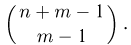Найдем теперь вероятность попадания в фиксированную ячейку ровно k частиц (событие А). Заметим, что если в этой фиксированной ячейке уже находится k частиц, то остальные 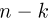частиц должны быть распределены по оставшимся 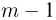ячейкам, а это, как мы знаем, можно сделать 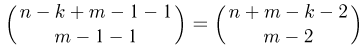способами. Следовательно, 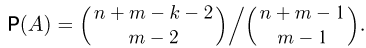Эйнштейна подчиняются фотоны, атомные ядра и атомы, содержащие четное число частиц.

Статистика Ферми-Дирака

В статистике Ферми-Дирака так же, как и в статистике Бозе-Эйнштейна, п неразличимых частиц распределяются по m ячейкам 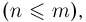однако в каждой ячейке не может находиться более одной частицы. Число различных размещений (элементарных исходов) совпадает с числом способов, которыми мы можем выбрать (без учета порядка выбора) п занятых ячеек из общего числа ячеек m т.е. равно 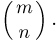Пусть событие А — заняты фиксированные k ячеек 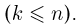Тогда оставшиеся 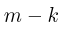ячеек должны быть заполнены 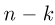частицами, а это можно сделать 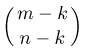способами. Поэтому 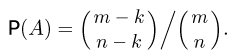Статистике Ферми-Дирака подчиняются электроны, протоны и нейтроны.

Статистика Максвелла-Больцмана

Предполагая, что n различных частиц распределяются по m ячейкам без ограничений на число попавших в каждую ячейку частиц, получаем статистику Максвелла-Больцмана. Поскольку каждая из n частиц может попасть в любую из т ячеек, то общее число элементарных исходов равно 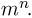Событие А заключается в том, что в первую ячейку попало 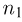частиц, во вторую — 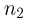частиц….. в m-ю — 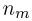частиц 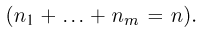Число благоприятных для события А исходов подсчитаем следующим образом. В первую ячейку могут попасть любые 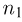частиц из n имеющихся первоначально. Поскольку порядок выбора частиц несуществен, то это можно сделать 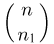способами. Как только первая ячейка заполнена, у нас остается 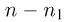частиц, и вторую ячейку мы можем заполнить 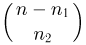различными способами. Продолжая эту процедуру и используя основную формулу комбинаторики, получаем, что число благоприятных событию А способов равно

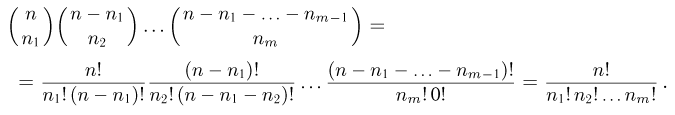
Таким образом,

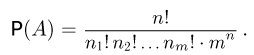
Отметим, что статистика Максвелла-Больцмана представляет собой частный случай так называемой полиномиальной схемы, которую мы рассмотри в параграфе 7 гл.4. Статистике Максвелла-Больцмана подчиняется идеальный газ.

Пример:

Поток из 4 частиц поступает в счетчик, состоящий из трех датчиков. Каждая частица с одинаковой вероятностью может попасть в один и только один из этих датчиков. Поток считается зарегистрированным, если он отмечен хотя бы двумя датчиками. Найдем вероятность события А, заключающегося в том, что поток будет зарегистрирован. Удобно перейти к дополнительному событию 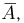которое происходит тогда и только тогда, когда все 4 частицы попадают либо в первый, либо во второй, либо в третий датчик. Но вероятность всем 4 частицам попасть в первый датчик определяется статистикой Максвелла-Больцмана, причем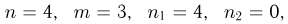 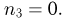Учитывая, что вероятность попадания всех 4 частиц во второй и третий датчики точно такая же, как и в первый, получаем

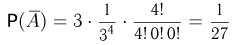
и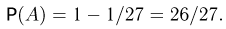

Решение заданий и задач по предметам:

• Теория вероятностей
• Математическая статистика

Дополнительные лекции по теории вероятностей:

1. Случайные события и их вероятности
2. Случайные величины
3. Функции случайных величин
4. Числовые характеристики случайных величин
5. Законы больших чисел
6. Статистические оценки
7. Статистическая проверка гипотез
8. Статистическое исследование зависимостей
9. Теории игр
10. Вероятность события
11. Теорема умножения вероятностей
12. Формула полной вероятности
13. Теорема о повторении опытов
14. Нормальный закон распределения
15. Определение законов распределения случайных величин на основе опытных данных
16. Системы случайных величин
17. Нормальный закон распределения для системы случайных величин
18. Вероятностное пространство
19. Геометрическая вероятность
20. Условная вероятность
21. Схема Бернулли
22. Многомерные случайные величины
23. Предельные теоремы теории вероятностей
24. Оценки неизвестных параметров
25. Генеральная совокупность