Оглавление:
Каждая наука, развивающая общую теорию какого-либо круга явлений, содержит ряд основных понятий, на которых она базируется. Таковы, например, в геометрии понятия точки, прямой, линии; в механике— понятия силы, массы, скорости, ускорения и т. д. Естественно, что не все основные понятия могут быть строго определены, так как определить понятие — это значит свести его к другим, более известным. Очевидно, процесс определения одних понятий через другие должен где-то заканчиваться, дойдя до самых первичных понятий, к которым сводятся все остальные и которые сами строго не определяются, а только поясняются.
Такие основные понятия существуют и в теории вероятностей. В качестве первого из них введем понятие события.
Под «событием» в теории вероятностей понимается всякий факт, который в результате опыта может произойти или не произойти.
Приведем несколько примеров событий: А — появление герба при бросании монеты; В — появление трех гербов при трехкратном бросании монеты; С — попадание в цель при выстреле; D—появление туза при вынимании карты из колоды; Е— обнаружение объекта при одном цикле обзора радиолокационной станции; F — обрыв нити в течение часа работы ткацкого станка.
Рассматривая вышеперечисленные события, мы видим, что каждое из них обладает какой-то степенью возможности: одни — большей, другие — меньшей, причем для некоторых из этих событий мы сразу же можем решить, какое из них более, а какое менее возможно. Например, сразу видно, что событие А более возможно, чем В и D. Относительно событий С, Е и F аналогичных выводов сразу сделать нельзя; для этого следовало бы несколько уточнить условия опыта. Так или иначе ясно, что каждое, из таких событий обладает той или иной степенью возможности. Чтобы количественно сравнивать между собой события по степени их возможности, очевидно, нужно с каждым событием связать определенное ч и с л о, которое тем больше, чем более возможно событие. Такое число мы назовем вероятностью события.
Таким образом, мы ввели в рассмотрение второе основное по- понятие теории вероятностей — понятие вероятности события. Вероятность события есть численная мера степени объективной возможности возможности этого события.
Заметим, что уже при самом введении понятия вероятности со- события мы связываем с этим понятием определенный практический смысл, а именно: на основании опыта мы считаем более вероятными те события, которые происходят чаще; менее вероятными —те события, которые происходят реже; мало вероятными — те, которые почти .никогда не происходят. Таким образом, понятие вероятности события в самой своей основе связано с опытным, практическим понятием частоты события.
Сравнивая между собой различные события по степени их воз- возможности, мы должны установить какую-то единицу измерения. В качестве такой единицы измерения естественно принять вероятность достоверного события, т. е. такого события, которое в результате опыта непременно должно произойти. Пример достоверного события — выпадение не более 6 очков при бросании одной игральной кости.
Если приписать достоверному событию вероятность, равную единице, то все другие события — возможные, но не достоверные — будут характеризоваться вероятностями, меньшими единицы, составляющими какую-то долю единицы.
Противоположностью по отношению к достоверному событию является невозможное событие, т. е. такое событие, которое в данном опыте не может произойти. Пример невозможного события — появление 12 очков при бросании одной игральной кости. Естественно приписать невозможному событию вероятность, равную нулю.
Таким образом, установлены единица измерения вероятностей — вероятность достоверного события — и диапазон изменения вероятностей любых событий —. числа от 0 до 1.
Непосредственный подсчет вероятностей
Существует целый класс опытов, для которых вероятности их возможных исходов легко оценить непосредственно из условий самого опыта. Для этого нужно, чтобы различные исходы опыта обладали симметрией и в силу этого были объективно одинаково возможными.
Рассмотрим, например, опыт, состоящий в бросании игральной кости, т. е. симметричного кубика, на гранях которого нанесено различное число очков; от 1 до 6.
В силу симметрии кубика есть основания считать все шесть воз- возможных исходов опыта одинаково возможными. Именно это дает нам право предполагать, что при многократном бросании кости все шесть граней будут выпадать примерно одинаково часто. Это предположение для правильно выполненной кости действительно оправдывается на опыте; при многократном бросании кости каждая ее грань появляется примерно в одной шестой доле всех случаев бросания, причем отклонение этой доли от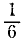 
тем меньше, чем большее число опытов произведено. Имея в виду, что вероятность достоверного события принята равной единице, естественно приписать выпадению каждой отдельной грани вероятность, равную 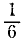Это число характеризует некоторые объективные свойства данного случайного явления, а именно свойство симметрии шести возможных исходов опыта.
Для всякого опыта, в котором возможные исходы симметричны и одинаково возможны, можно применить аналогичный прием, который называется непосредственным подсчетом вероятностей.
Симметричность возможных исходов опыта обычно наблюдается только в искусственно организованных опытах, типа азартных игр. Так как первоначальное развитие теория вероятностей получила именно на схемах азартных игр, то прием непосредственного под- подсчета вероятностей, исторически возникший вместе с возникновением математической теории случайных явлений, долгое время считался основным и был положен в основу так называемой «классической» теории вероятностей. При этом опыты, не обладающие симметрией возможных исходов, искусственно сводились к «классической» схеме.
Несмотря на ограниченную сферу практических применений этой схемы, она все же представляет известный интерес, так как именно на опытах, обладающих симметрией возможных исходов, и на событиях, связанных с такими опытами, легче всего познакомиться с основными свойствами вероятностей. Такого рода событиями, допускающими непосредственный подсчет вероятностей, мы и займемся в первую очередь.
Предварительно введем некоторые вспомогательные понятия.
- Полная группа событий. Говорят, что несколько событий в данном опыте образуют полную группу событий, если в результате опыта непременно должно появиться хотя бы одно из них.
Примеры событий’, образующих полную группу: 1) выпадение герба и выпадение цифры при бросании монеты; 2) попадание и промах при выстреле; 3) появление 1,2, 3, 4, 5, 6 очков при бросании игральной кости; 4) появление белого шара и появление черного шара при вынимании одного шара из урны, в которой 2 белых и 3 черных шара; 5) ни одной опечатки, одна, две, три и более трех опечаток при проверке страницы напечатанного текста;
6) хотя бы одно попадание и хотя бы одни промах при двух выстрелах.
Несовместные события
Несколько событий называются несовместными в данном опыте, если никакие два из них не могут появиться вместе. Примеры несовместных событий: 1) выпадение герба и выпадение цифры при бросании монеты; 2) попадание и промах при одном выстреле; 3) появление 1, 3, 4 очков при одном бросании игральной кости; 4) ровно один отказ, ровно два отказа, ровно три отказа тех- технического устройства за десять часов работы.
Равновозможные события
Несколько событий в данном опыте называются равновозмож- ными, если по условиям симметрии есть основание считать, что ни одно из этих событий не является объективно более возможным, чем другое. Примеры равновозможных событий: 1) выпадение герба и выпадение цифры при бросании монеты; 2) появление 1, 3, 4, 5 очков при бросании игральной кости; 3) появление карты бубновой, червонной, трефовой масти при вынимании карты из колоды; 4) появление шара с № 1, 2, 3 при вынимании одного шара из урны, содержащей 10 перенумерованных шаров.
Существуют группы событий, обладающие всеми тремя свойствами: они образуют полную группу, несовместны и равновозможны; на- например: появление герба и цифры при бросании монеты; появление 1, 2, 3, 4, 5, 6 очков при бросании игральной кости. События, образующие такую группу, называются случаями (иначе «шансами»).
Если какой-либо опыт по своей структуре обладает симметрией возможных исходов, то случаи представляют собой исчерпывающую систему равновозможных и исключающих друг друга исходов опыта. Про такой опыт говорят, что он «сводится к схеме случаев» (иначе — к «схеме урн»).
Схема случаев по преимуществу имеет место в искусственно ор- организованных опытах, в которых заранее и сознательно обеспечена одинаковая возможность исходов опыта (как, например, в азартных играх). Для таких опытов возможен непосредственный подсчет вероятностей, основанный на оценке доли так называемых «благоприятных» случаев в общем числе случаев.
Случай называется благоприятным (или «благоприятствующим») некоторому событию, если появление этого случая влечет за собой появление данного события.
Например, при бросании игральной кости возможны шесть случаев: появление 1, 2, 3, 4, 5, 6 очков. Из них событию А—появлению четного числа очков — благоприятны три случая: 2, 4, б и не благоприятны остальные три.
Если опыт сводится к схеме, случаев, то вероятность события А в данном опыте можно оценить по относительной дело благоприятных случаев. Вероятность события А вычисляется как отношение числа благоприятных случаев к общему числу случаев: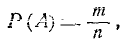 
(2.2.1)
где Р (А) — вероятность события А; п — общее число случаев; m — число случаев, благоприятных событию А.
Так как число благоприятных случаев всегда заключено между О и п (0—для невозможного и п—для достоверного события), то вероятность события, вычисленная по формуле 2.2.1), всегда есть рациональная правильная дробь: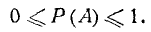 
(2.2.2)
Формула (2.2.1), так называемая «классическая формула» для вы- вычисления вероятностей, долгое время фигурировала в литературе как определение вероятности. В настоящее время при определении (пояснении) понятия вероятности обычно исходят из других принципов, непосредственно связывая понятие вероятности с эмпирическим понятием частоты; формула же B.2.1) сохраняется лишь как формула для непосредственного подсчета вероятностей, пригодная тогда и только тогда, когда опыт сводится к схеме случаев, т. е. обладает симметрией возможных исходов.
Пример:
В урне находится 2 белых и 3 черных шара. Из урны на- наугад вынимается один шар. Требуется найти вероятность того, что этот шар будет белым.
Решение:
Обозначим А событие, состоящее в появлении белого шара. Общее число случаев п= 5; число случаев, благоприятных событию А, m = 2. Следовательно,
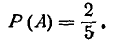
Пример:
В урне а белых и b черных шаров. Из урны вынимаются два шара. Найти вероятность того, что оба шара будут белыми.
Решение:
Обозначим В событие, состоящее в появлении двух белых шаров. Подсчитаем общее число возможных случаев п и число случаев m благоприятных событию В:
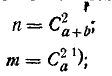
следовательно,
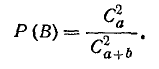
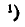Знаком 
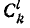обозначено число сочетаний из k элементов по l
Пример:
В партии из N изделий М бракованных. Из партии выбирается наугад п изделий. Определить вероятность того, что среди этих п изделий будет ровно m бракованных.
Решение:
Общее число случаев, очевидно, равно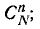 
число благо- благоприятных случаев 
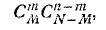откуда вероятность интересующего нас события
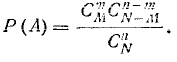
Частота, или статистическая вероятность, события
Формула (2.2.1) для непосредственного подсчета вероятностей применима только, когда опыт, в результате которого может появиться интересующее нас событие, обладает симметрией возможных исходов (сводится к схеме случаев). Очевидно, что далеко не всякий опыт может быть сведен к схеме случаев, и существует обширный класс событий, вероятности которых нельзя вычислить по формуле (2.2.1). Рассмотрим, например, неправильно выполненную, несимметричную игральную кость. Выпадение определенной грани уже не будет характеризоваться вероятностью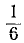 
; вместе с тем ясно, что для данной конкретной несимметричной кости выпадение этой грани обладает некоторой вероятностью, указывающей, насколько часто в среднем должна появляться данная грань при многократном бросании. Очевидно, что вероятности таких событий, как «попадание в цель при выстреле», «выход из строя радиолампы в течение од- одного часа работы» или «пробивание брони осколком снаряда», так- также не могут быть вычислены по формуле (2.2.1) , так как соответствующие опыты к схеме случаев не сводятся. Вместе с тем ясно, что каждое из перечисленных событий обладает определенной степенью объективной возможности, которую в принципе можно измерить численно и которая при повторении подобных опытов будет отражаться в относительной частоте соответствующих событий. Поэтому мы будем считать, что каждое событие, связанное с массой однородных опытов,—сводящееся к схеме случаев или нет,—имеет определенную вероятность, заключенную между нулем и единицей. Для событий, сводящихся к схеме случаев, эта вероятность может быть вычислена непосредственно по формуле B.2.1). Для событий, не сводящихся к схеме случаев, применяются другие способы определения вероятностей. Все эти способы корнями своими уходят в опыт, в эксперимент, и для того чтобы составить представление об этих способах, необходимо уяснить себе понятие частоты события и специфику той органической связи, которая существует между вероятностью и частотой.
[Если произведена серия из п опытов, в каждом из которых могло появиться или не появиться некоторое событие А, то частотой события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу произведен- произведенных опытов.
Частоту события часто называют его статистической вероятностью (в отличие от ранее введенной «математической» вероятности).
Условимся обозначать частоту (статистическую вероятность) со- события А знаком Р* (А). Частота события вычисляется на основании результатов опыта по формуле
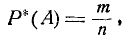(2.3.1)
где m — число появлений события А; п — общее число произведен- произведенных опытов.
При небольшом числе опытов частота события носит в значительной мере случайный характер и может заметно изменяться от одной группы опытов к другой. Например, при каких-то десяти бросаниях монеты вполне возможно, что герб появится только два раза (частота появления герба будет равна 0,2); при других десяти бросаниях мы вполне можем получить 8 гербов (частота 0,8). Однако при увеличении числа опытов частота события все более теряет свой случайный характер; случайные обстоятельства, свойственные каждому отдельному опыту, в массе взаимно погашаются, и частота проявляет тенденцию стабилизироваться, приближаясь с незначительными колебаниями к некоторой средней, постоянной величине. Например, при многократном бросании монеты частота появления герба будет лишь незначительно уклоняться от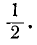 
Это свойство «устойчивости частот», многократно проверенное экспериментально и подтверждающееся всем опытом практической деятельности человечества, есть одна из наиболее характерных за- закономерностей, наблюдаемых в случайных явлениях. Математическую формулировку этой закономерности впервые дал Я. Бернулли в своей теореме, которая представляет собой простейшую форму закона больших чисел. Я. Бернулли доказал, что при неограниченном увеличении числа однородных независимых опытов с практической достоверностью можно утверждать, что частота события будет сколь угодно мало отличаться от его вероятности в отдельном опыте.
Связь между частотой события и его вероятностью — глубокая, органическая связь. Эти два понятия по существу неразделимы. Дей- Действительно, когда мы оцениваем степень возможности какого-либо события, мы неизбежно связываем эту оценку с большей или меньшей частотой появления аналогичных событий на практике. Характеризуя вероятность события каким-то числом, мы не можем придать этому числу иного реального значения и иного практического смысла, чем относительная частота появления данного события при большом числе опытов. Численная оценка степени возможности события посредством вероятности имеет практический смысл именно потому, что более вероятные события происходят в среднем чаще, чем менее вероятные. И если практика определенно указывает на то, что при увеличении числа опытов частота события имеет тенденцию выравниваться, приближаясь сквозь ряд случайных уклонений к некоторому постоянному числу, естественно предположить, что это число и есть вероятность события.
Проверить такое предположение мы, естественно, можем только для таких событий, вероятности которых могут быть вычислены непосредственно, т. е. для событий, сводящихся к схеме случаев, так как только для этих событий существует точный способ вычисления математической вероятности. Многочисленные опыты, производившиеся со времени возникновения теории вероятностей, действительно подтверждают это предположение. Они показывают, что для события, сводящегося к схеме случаев, частота события при увеличении числа опытов всегда приближается к его вероятности. Вполне естественно допустить, что и для события, не сводящегося к схеме случаев, тот же закон остается в силе и что постоянное значение, к которому при увеличении числа опытов приближается частота события, представляет собой не что иное, как вероятность события. Тогда частоту события при достаточно большом числе опытов можно принять за приближенное значение вероятности. Так и поступают на практике, определяя из опыта вероятности событий, не сводящихся к схеме случаев.
Следует отметить, что характер приближения частоты к вероятности при увеличении числа опытов несколько отличается от «стремления к пределу» в математическом смысле слова.
Когда в математике мы говорим, что переменная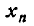 
с возраста- возрастанием n стремится к постоянному пределу а, то это означает, что разность 
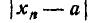становится меньше любого положительного числа 
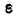для всех значений п, начиная с некоторого достаточно большого числа.
Относительно частоты события и его вероятности такого категорического утверждения сделать нельзя. Действительно, нет ничего физически невозможного в том, что при большом числе опытов частота события будет значительно уклоняться от его вероятности; но такое значительное уклонение является весьма маловероятным, тем менее вероятным, чем большее число опытов произведено. Например, при бросании монеты 10 раз физически возможно (хотя и маловероятно), что все 10 раз появится герб, и частота появления герба будет равна 1; при 1000 бросаниях такое событие все еще остается физически возможным, но приобретает настолько малую вероятность, что его смело можно считать практически неосуществимым. Таким образом, при возрастании числа опытов частота приближается к вероятности, но не с полной достоверностью, а с большой вероятностью, которая при достаточно большом числе опытов может рассматриваться как практическая достоверность.
В теории вероятностей чрезвычайно часто встречается такой характер приближения одних величин к другим, и для его описания введен специальный термин: «сходимость по вероятности».
Говорят, что величина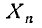 
сходится по вероятности к величине а, если при сколь угодно малом е вероятность неравенства 
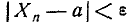с увеличением п неограниченно приближается к единице.
Применяя этот термин, можно сказать, что при увеличении числа опытов, частота события не «стремится.» к вероятности события, а «сходится к ней по вероятности»
Это свойство частоты и вероятности, изложенное здесь пока без достаточных математических оснований, просто на основании практики и здравого смысла, составляет содержание теоремы Бернулли, которая будет доказана нами в дальнейшем (см. гл. 13).
Таким образом, вводя понятие частоты события и пользуясь связью между частотой и вероятностью, мы получаем возможность приписать определенные вероятности, заключенные между нулем и единицей, не только событиям, которые сводятся к схеме случаев, но и тем событиям, которые к этой схеме не сводятся; в последнем случае вероятность события может быть приближенно определена по частоте события при большом числе опытов.
В дальнейшем мы увидим, что для определения вероятности со- события, не сводящегося к схеме случаев, далеко не всегда необходимо непосредственно определять из опыта его частоту. Теория вероятностей располагает многими способами, позволяющими определять вероятности событий косвенно, через вероятности других событий, с ними связанных. В сущности, такие косвенные способы и составляют основное содержание теории вероятностей. Однако и при таких косвенных методах исследования в конечном счете все же приходится обращаться к экспериментальным данным. Надежность и объективная ценность всех практических расчетов, выполненных с применением аппарата теории вероятностей, определяется качеством и количеством экспериментальных данных, на базе которых этот расчет выполняется.
Кроме того, при практическом применении вероятностных методов исследования всегда необходимо отдавать себе отчет в том, действительно ли исследуемое случайное явление принадлежит к категории массовых явлений, для которых, по крайней мере на некотором участке времени, выполняется свойство устойчивости частот. Только в этом случае имеет смысл говорить о вероятностях событий, имея в виду не математические фикции, а реальные характеристики случайных явлений.
Например, выражение «вероятность поражения самолета в воз- воздушном бою для данных условий равна 0,7» имеет определенный конкретный смысл, потому что воздушные бои мыслятся как массовые операции, которые будут неоднократно повторяться в приблизительно аналогичных условиях.
Напротив, выражение «вероятность того, что данная научная про- проблема решена правильно, равна 0,7» лишено конкретного смысла, и было бы методологически неправильно оценивать правдоподобие научных положений метопами теории вероятностей.
Случайная величина
Одним из важнейших основных понятий теории вероятностей является понятие о случайной величине. Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.
Примеры случайных величин: 1) число попаданий при трех выстрелах; 2) число вызовов, поступавших на телефонную станцию за сутки; 3) частота попадания при 10 выстрелах. Во всех трех приведенных примерах случайные величины могут принимать отдельные, изолированные значения, которые можно заранее перечислить.
Так,в примере 1) эти значения: 0, 1, 2, 3; в примере 2): 1, 2, 3, 4, …; в примере 3): 0; 0,1; 0,2; …; 1,0.
Такие случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить называются прерывными или дискретными случайными величинами.
Существуют случайные величины другого типа, например: 1) абсцисса точки попадания при выстреле; 2) ошибка взвешивания тела на аналитических весах; 3) скорость летательного аппарата в момент выхода на заданную высоту; 4) вес наугад взятого зерна пшеницы.
Возможные значения таких случайных величин не отделены друг от друга; они непрерывно заполняют некоторый промежуток, кото- который иногда имеет резко выраженные границы, а чаще —границы неопределенные, расплывчатые.
Такие случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, называются непрерывными случайными величинами.
Такие случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, называются непрерывными случайными величинами.
Приведем примеры типичных для теории вероятностей приемов перехода от событий к случайным величинам. Производится опыт, в результате которого может появиться или не появиться некоторое событие А. Вместо события А можно рассмотреть случайную величину X, которая равна 1, если событие А происходит, и равна 0, если событие А не происходит. Случайная величина А‘, очевидно, является прерывной; она имеет два возможных значения: 0 и 1. Эта случайная величина называется характеристической случайной величиной события А. На практике часто вместо событий оказывается удобнее оперировать их характеристическими случайными величинами. Например, если производится ряд опытов, в каждом из которых возможно появление события А, то общее число появлений события равно сумме характеристических случайных величин события А во всех опытах. При решении многих практических задач пользование таким приемом оказывается очень удобным.
С другой стороны, очень часто для вычисления вероятности события оказывается удобно связать это событие с какой-то непрерывной случайной величиной (или системой непрерывных величин)
Пусть, например, измеряются координаты какого-то объекта О для того, чтобы построить точку М, изображающую этот объект на панораме (развертке) местности. Нас интересует событие А, состоящее в том, что ошибка R в положении точки М не превзойдет заданного значения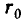 
(рис. 2.4.1). Обозначим X, Y случайные ошибки в измерении координат объекта. Очевидно, событие А равносильно попаданию случайной точки М с координатами X, Y в пределы круга радиуса 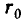с центром в точке О. Другими словами, для выполнения события А случайные величины X и К должны удовлетворять неравенству
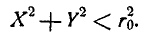(2.4.1)
Вероятность события А есть не что иное, как вероятность выполнения неравенства B.4.1). Эта вероятность может быть определена, если известны свойства случайных величин X, Y.
Такая органическая связь между событиями и случайными вели- величинами весьма характерна для современной теории вероятностей, которая, где только возможно, переходит от «схемы событий» к «схеме случайных величин». Последняя схема сравнительно с первой представляет собой гораздо более гибкий и универсальный аппарат для решения задач, относящихся к случайным явлениям.
Практически невозможные и практически достоверные события. Принцип практической уверенности
Мы познакомились с понятиями невозможного и достоверного события. Вероятность невозможного события, равная нулю, и вероятность достоверного события, равняя единице, занимают крайние положения на шкале вероятностей.
На практике часто приходится иметь дело не с невозможными и достоверными событиями, а с так называемыми «практически невозможными» и «практически достоверными» событиями.
Практически невозможным событием называется событие, вероятность которого не в точности равна нулю, но весьма близка к нулю.
Рассмотрим, например, следующий опыт: 32 буквы разрезной азбуки смешаны между собой; вынимается одна карточка, изображенная на ней буква записывается, после чего вынутая карточка возвращается обратно, и карточки перемешиваются. Такой опыт производится 25 раз. Рассмотрим событие А, заключающееся в том, после 25 выниманий мы запишем первую строку «Евгения Онегина»:
«Мой дядя самых честных правил».
Такое событие не является логически невозможным; можно под- считать его вероятность, которая равна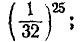 
но ввиду того что вероятность события А ничтожно мала, можно считать его практически невозможным.
Практически достоверным событием называется событие, вероятность которого не в точности равна единице, но весьма близка к единице.
Если какое-либо событие А в данном опыте практически невозможно, то противоположное ему событие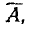 
состоящее в невыполнении события А, будет практически достоверным. Таким образом, с точки зрения теории вероятностей все равно, о каких событиях говорить: о практически невозможных или о практически достоверных, так как они всегда сопутствуют друг другу.
Практически невозможные и практически достоверные события играют большую роль в теории вероятностей; на них основывается все практическое применение этой науки.
В самом деле, если нам известно, что вероятность события в дан- данном опыте равна 0,3, это еще не дает нам возможности предсказать результат опыта. Но если вероятность события в данном опыте ничтожно мала или, наоборот, весьма близка к единице, это дает нам возможность предсказать результат опыта; в первом случае мы не будем ожидать появления события А; во втором случае будем ожидать его с достаточным основанием. При таком предсказании мы руководствуемся так называемым принципом практической уверенности, который можно сформулировать следующим образом.
Если вероятность некоторого события А в данном опыте Е весьма мала, то можно быть практически уверенным в том, что при однократном выполнении опыта Е событие А не произойдет.
Иными словами, если вероятность события А в данном опыте весьма мала, то, приступая к выполнению опыта, можно организовать свое поведение так, как будто это событие вообще невозможно, т. е. не рассчитывал совсем на его появление.
В повседневной жизни мы непрерывно бессознательно пользуемся принципом практической уверенности. Например, выезжая в путешествие по железной дороге, мы все свое поведение организуем, не считаясь с возможностью железнодорожной катастрофы, хотя некоторая, весьма малая, вероятность такого события все же имеется.
Принцип практической уверенности не может быть доказан мате- математическими средствами; он подтверждается всем практическим опытом человечества.
Вопрос о том, насколько мала должна быть вероятность события, чтобы его можно было считать практически невозможным, выходит за рамки математической теории и в каждом отдельном случае ре- решается из практических соображений в соответствии с той важностью, которую имеет для нас желаемый результат опыта.
Например, если вероятность отказа взрывателя при выстреле равна 0,01, мы еще можем помириться с этим и считать отказ взрывателя практически невозможным событием. Напротив, если вероятность отказа парашюта при прыжке также равна 0,01, мы, очевидно, не можем считать этот отказ практически невозможным событием и должны добиваться большей надежности работы парашюта.
Одной из важнейших задач теории вероятностей является выявление практически невозможных (или практически достоверных) событий, дающих возможность предсказывать результат опыта, и выявление условий, при которых те или иные события становятся практически невозможными (достоверными). Существует ряд теорем теории вероятностей — так называемых предельных теорем, в которых устанавливается существование, событий, становящихся практически невозможными (достоверными) при увеличении числа опытов или при увеличении числа случайных величин, участвующих в задаче.
Примером такой предельной теоремы является уже сформулированная выше теорема Бернулли (простейшая форма закона больших чисел). Согласно теореме Бернулли при большом числе опытов событие, заключающееся в том, что разность между частотой события и его вероятностью сколь угодно мала, становится практически достоверным.
Наряду с практически невозможными (достоверными) событиями, которые позволяют с уверенностью предсказывать исход опыта, не- несмотря на наличие случайности, в теории вероятностей большую роль играют особого типа случайные величины, которые, хотя и являются случайными, но имеют такие незначительные колебания, что практически могут рассматриваться как не случайные. Примером такой «почти не случайной» величины может служить частота события при большом числе опытов. Эта величина, хотя и является случайной, но при большом числе опытов практически может колебаться только в очень узких пределах вблизи вероятности события.
Такие «почти не случайные» величины дают возможность пред- предсказывать численный результат опыта, несмотря на наличие в нем элементов случайности, оперируя с этим результатом столь же уверенно, как мы оперируем с данными, которые доставляются обычными методами точных наук.
Решение заданий и задач по предметам:
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность
