Уравнение Бернулли для установившегося потока газа

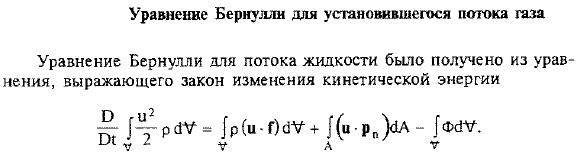
Уравнение Бернулли для установившегося потока газа

Уравнение Бернулли для установившегося потока газа. Уравнение Бернулли для течения жидкости было выведено из уравнения, представляющего закон изменения кинематической энергии Как уже говорилось выше, для описания движения газа необходимо учитывать внутреннюю энергию жидкости. Это прежде всего кинетическая энергия хаотического теплового движения молекул газа. (4.20). Где e (r, {) плотность распределения внутренней (тепловой) энергии газа или внутренней энергии удельного (на единицу массы) газа.

Поэтому для получения уравнения Бернулли течения газа необходимо исходить из более общего уравнения, представляющего собой закон сохранения энергии контролируемого объема сплошной среды. Людмила Фирмаль

• Плотность распределения в пределах контролируемого объема теплового источника (на единицу объема в единицу времени). a (g, g) плотность распределения на управляющей поверхности источника тепла (на единицу площади в единицу времени). \ Y; мощность точечного источника (стока) энергии в управляющем объеме. Если в контрольном объеме (дисперсия m = 0, точка= 0) и на его поверхности (o = 0) отсутствует внешний источник тепловой и механической энергии (сток), то формула (15.14) отличается от формулы. Кроме плотности распределения кинетической энергии по левому интегралу уравнения, наличие плотности распределения e (r, {) внутренней энергии в виде членов.

• Отсутствует термин, обозначающий силу внутренних сил (диссипацию механической энергии)в управляющем объеме. Заметим, что за счет работы внутренних сил внутренняя энергия жидкости увеличивается (см. раздел 4.6).Вы хотите выполнить все преобразования, показанные в этом разделе. 5.4, используя в качестве начального уравнения (15.14) вместо уравнения Бернулли (5.40) По сравнению с (5.40), термин e отображался и не отображался / ФС№. кроме того, вывод этого уравнения имеет и следующее содержание, и все гидродинамические свойства (u, e, p, p) постоянны при каждом вычисленном поперечном сечении живого тела, cc = 1.0 и = V.

Почти всегда гравитационная работа газового потока имеет незначительный вклад в энергетический баланс. Людмила Фирмаль

• Уменьшение 3M даст уравнение Бернулли искомого газа. Уравнение при учете течения невязкого газа и тем самым исключении движения механической энергии поперек потока за счет вязкости 274 (15.16) применим не только к сплошным стеновым потокам, но и к токовым трубам с постоянным массовым расходом 0 м. В связи с тем, что поперечные размеры токовой трубы могут быть сколь угодно малы, формула (15.16) может быть использована для любых 2 точек, находящихся на одном потоке line. In другими словами, из Формулы (15.16) следует уравнение Он эффективен вдоль потока с устойчивым движением газа.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Дифференциальные уравнения, выражающие закон изменения кинетической энергии.
2. Скорость распространения возмущений сжимаемой среде.
3. Краткие сведения из термодинамики.
4. Зависимость скорости звука от термодинамических условий. Термодинамические формы уравнения Бернулли.