Оглавление:
Методы оценивания параметров структурной модели. Косвенный метод наименьших квадратов. Двухшаговый метод наименьших квадратов
Раньше отмечалось, что если выполняются предпосылки применения МНК, то оценки параметров функции регрессии являются несмещенными, эффективными и состоятельными. МНК применяется и для оценки параметров некоторых структурных коэффициентов. Так, например, применение МНК для оценки структурных коэффициентов рекурсивной модели дает состоятельные оценки при соблюдении определенной последовательности действий. Сначала оцениваются параметры первого уравнения, в правой части которого содержатся только предопределенные переменные, т. е. эндогенная переменная 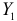 зависит только от экзогенных переменных
зависит только от экзогенных переменных 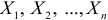 и возмущающей переменной
и возмущающей переменной 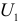 . Найденное значение
. Найденное значение 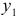 подставляется во второе уравнение, т. е. она становится предопределенной переменной. Затем оцениваются параметры второго уравнения и т.д.
подставляется во второе уравнение, т. е. она становится предопределенной переменной. Затем оцениваются параметры второго уравнения и т.д.
Метод наименьших квадратов не может применяться к оценке параметров структурных уравнений, так как они не учитывают одновременных соотношений между совместно зависимыми переменными. Поскольку в результате непосредственного применения МНК для каждого из уравнений модели получаем смещенные и несостоятельные оценки параметров, то разработан косвенный метод наименьших квадратов получения оценок, основанный на использовании приведенных уравнений.
Рассмотрим применение этого метода для кейнсианской модели формирования доходов (6.4) — (6.5). В приведенной форме эта модель выражается в виде двух уравнений (6.15) — (6.16):
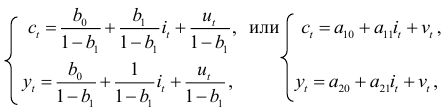
где
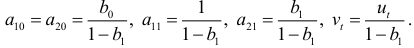
Поскольку объем инвестиций 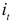 является экзогенной переменной и, следовательно, переменная
является экзогенной переменной и, следовательно, переменная 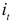 не коррелирует со случайными переменными
не коррелирует со случайными переменными 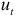 то для
то для 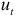 или
или 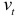 выполняются предпосылки МНК. Применив метод наименьших квадратов для определения коэффициентов
выполняются предпосылки МНК. Применив метод наименьших квадратов для определения коэффициентов 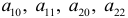 , несложно найти значения коэффициентов
, несложно найти значения коэффициентов 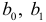 по формулам:
по формулам:
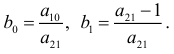
Определение оценок посредством преобразований уравнений к приведенной форме называется косвенным методом наименьших квадратов (КМНК).
Оценки, полученные по КМНК, являются состоятельными и они получаются однозначно, а соответствующее уравнение называется идентифицируемым (однозначно определенным).
Устранить коррелированность эндогенных переменных со случайным отклонением можно при помощи введения инструментальной переменной (ИП) 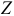 , удовлетворяющей следующим свойствам: она должна коррелировать с заменяемой эндогенной переменной
, удовлетворяющей следующим свойствам: она должна коррелировать с заменяемой эндогенной переменной  , но не коррелировать со случайными отклонениями
, но не коррелировать со случайными отклонениями 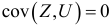 .
.
Так в структурном уравнении функции потребления (6.4) модели Кейнса, в качестве инструментальной переменной для 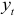 можно использовать
можно использовать 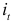 .
.
Полученные оценки 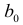 и
и 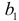 МНК, при использовании инструментальной переменной /,, будут состоятельными оценками.
МНК, при использовании инструментальной переменной /,, будут состоятельными оценками.
Рассмотрим еще один метод оценивания параметров, который учитывает многосторонние связи совместно зависимых переменных — двухшаговый метод наименьших квадратов (ДМНК). Суть этого метода состоит в поэтапном применении обычного метода наименьших квадратов для оценивания параметров структурного уравнения. Он применяется для нахождения инструментальной переменной, если в уравнении имеется избыток экзогенных переменных, которые можно использовать как инструментальные. На первом шаге ДМНК оценивается переопределенная переменная, опираясь лишь на экзогенные переменные. На втором этапе подставляем полученную оценку переопределенной переменной в исходную модель и получаем систему приведенных уравнений, для оценки параметров которой (приведенной системы) применяем МНК. В результате получаем состоятельные оценки структурных коэффициентов. При наличии в модели более одной переопределенной переменной на первом этапе необходимо оценить все такие переменные, выразив их через экзогенные и предопределенные переменные.
Пример 6.1.
Рассмотрим эмпирические данные, характеризующие ВНП 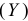 , потребление
, потребление 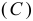 и инвестиции
и инвестиции 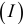 , таблица 6.1.
, таблица 6.1.

Предположим, что изучается закрытая экономика без государственных расходов, описываемая кейнсианской моделью:
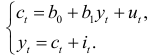
Оценим параметры 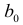 и
и 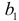 на основе КМНК. Решение. В п. 6.2 было показано, что модель Кейнса идентифицируема (количество уравнений, связывающих коэффициенты, равно количеству коэффициентов). Применив МНК для оценки параметров
на основе КМНК. Решение. В п. 6.2 было показано, что модель Кейнса идентифицируема (количество уравнений, связывающих коэффициенты, равно количеству коэффициентов). Применив МНК для оценки параметров 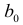 и
и 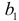 первого уравнения, описывающего функцию потребления, получим:
первого уравнения, описывающего функцию потребления, получим:
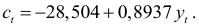
Если же применить косвенный метод наименьших квадратов, то получим следующее уравнение:
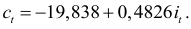
В данном уравнении потребление выражается через экзогенную переменную 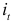 , характеризующую инвестиции. В первом случае, потребление выражено через эндогенную переменную
, характеризующую инвестиции. В первом случае, потребление выражено через эндогенную переменную 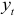 , которая в свою очередь выражается через потребление и инвестиции. Применив формулы
, которая в свою очередь выражается через потребление и инвестиции. Применив формулы
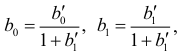
находим значения структурных коэффициентов исходной модели
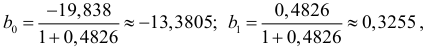
которые являются несмещенными и состоятельными оценками. Следовательно, кейнсианская модель имеет вид:
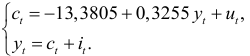
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

