Линейная частная регрессия
Из приведенных выше рассуждений следует, что в множественной регрессии исследуется одновременное влияние нескольких 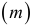 факторных признаков
факторных признаков 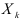 на результативный признак
на результативный признак 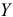 . При этом указывалось, что коэффициент множественной регрессии
. При этом указывалось, что коэффициент множественной регрессии 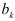 выражает частное влияние фактора
выражает частное влияние фактора 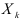 на результативный признак
на результативный признак 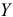 при постоянных значениях других факторов. Это означает, что между множественной и частной регрессиями нет разницы. Покажем это для трех связанных между собой переменных
при постоянных значениях других факторов. Это означает, что между множественной и частной регрессиями нет разницы. Покажем это для трех связанных между собой переменных 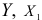 и
и 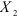 . Предположим, что между переменными
. Предположим, что между переменными 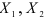 и
и 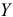 существуют линейные соотношения. Представим частную регрессию
существуют линейные соотношения. Представим частную регрессию 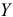 на
на 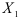 при исключении
при исключении 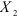 . Для этого вначале найдем простые регрессии
. Для этого вначале найдем простые регрессии 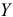 на
на 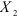 и
и 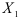 на
на 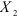 . Они выразятся следующими уравнениями:
. Они выразятся следующими уравнениями:
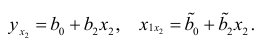
Из систем нормальных уравнений для указанных регрессий можно найти 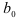 и
и 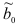 :
:
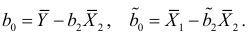
Тогда уравнения регрессий выразятся формулами:
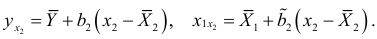
Предположим теперь, что переменная 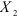 изъята из анализа. В этом случае регрессия
изъята из анализа. В этом случае регрессия 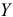 на
на 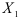 определяется по данным
определяется по данным 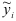 и
и 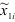 из которых исключено влияние
из которых исключено влияние 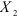 :
:
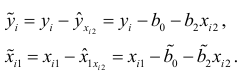
Так как средние арифметические переменных 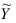 и
и 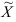 равны нулю, то уравнение регрессии по данным, из которых исключено влияние
равны нулю, то уравнение регрессии по данным, из которых исключено влияние 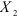 , имеет вид:
, имеет вид:
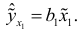
Регрессия переменных с исключением влияния 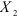 определяется коэффициентом
определяется коэффициентом 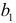 называемым коэффициентом частной регрессии.
называемым коэффициентом частной регрессии.
Применив метод наименьших квадратов для нахождения оценки неизвестного параметра 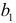 , получим
, получим
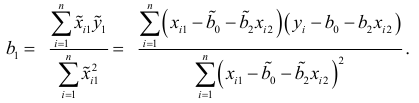
Выполняя в приведенной формуле ряд алгебраических операций, приходим к выражению, аналогичному (2.6). Этот факт подтверждает, что частная регрессия не приводит к новым результатам при исследовании зависимостей.
Итак, при изучении регрессии нет необходимости различать частную и множественную регрессии, так как коэффициенты частной регрессии совпадают с соответствующими коэффициентами множественной регрессии.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

