Многофакторная линейная регрессионная модель в нормированной размерности
В случае множественной регрессии более чем с двумя независимыми переменными выполняют нормирование переменных по формулам:
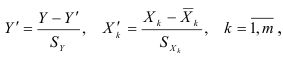
где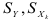 
— стандартные отклонения переменных 
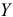и 
.
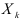Проведенное нормирование позволяет упрощать расчеты определений оценок неизвестных параметров, так как исключается свободный член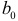 
и за начало отсчета каждой переменной принимается значение среднего, а за единицу измерения — значение стандартного отклонения. Уравнение множественной линейной регрессии в нормированной размерности приобретает вид
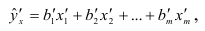
где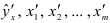 
— значения нормированных переменных; 
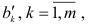-нормированные коэффициенты регрессии.
Оценки 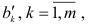нормированных коэффициентов множественной регрессии находим методом наименьших квадратов. Из соответствующих формул следуют соотношения между обычными и нормированными коэффициентами регресси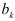и 
и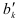 
:
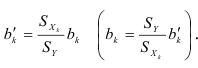
Как отмечалось выше, коэффициенты регрессии 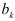имеют размерность переменной 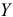, деленную на размерность переменной 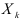. Поэтому любое изменение единицы переменной величины сказывается на коэффициенте регрессии. Из формул (2.7 и (2.8) следует, что нормированные переменные 
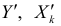и нормированные коэффициенты регрессии 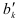безразмерны. Вследствие этого становится возможным сравнение факторных переменных при оценке интенсивности их влияния на результативный признак, так как нормированные переменные выражаются в единицах стандартных отклонений.
Нормированные коэффициенты множественной регрессии характеризуют скорость изменения среднего значения результативного признака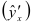 
по каждому факторному признаку 
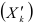при постоянных значениях остальных факторов, включенных в модель. Они показывают, на какую часть стандартного отклонения изменилось бы среднее значение результативного признака, если бы значение факторного признака увеличилось на стандартное отклонение, а прочие факторы остались без изменения.
Таким образом, нормированные коэффициенты регрессии показывают сравнительную силу влияния каждого фактора-признака на изменение результативного признака.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
| Пример построения однофакторной регрессионной модели |
| Построение многофакторной линейной регрессионной модели |
| Линейная частная регрессия |
| Отбор важнейших факторов многофакторных регрессионных моделей |
