Задача 1.67.
Машиностроительное предприятие для изготовления четырех видов продукции использует токарное, фрезерное, сверлильное, расточное и шлифовальное оборудование, а также комплектующие изделия. Кроме того, сборка изделий требует выполнения определенных сборочно-наладочных работ. Нормы затрат всех видов ресурсов на изготовление каждого из изделий приведены в табл. 1.39. В этой же таблице указаны наличный фонд каждого из ресурсов, прибыль от реализации единицы продукции данного вида, а также ограничения на возможный выпуск продукции 2-го и 3-вида.
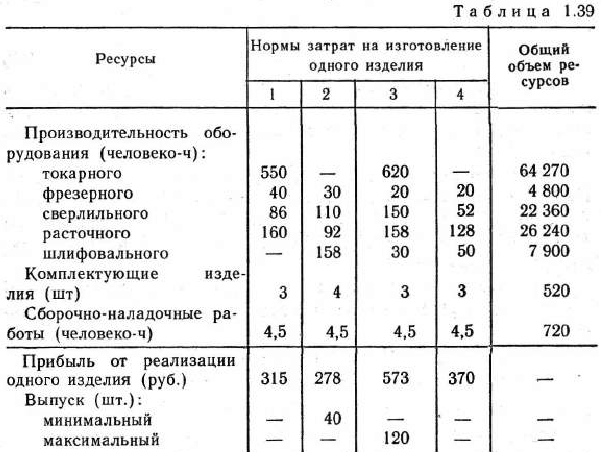
Найти план выпуска продукции, при котором прибыль от ее реализации является максимальной.
Решение:
Составим математическую модель задачи. Предположим, что предприятие изготовит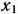 
изделий 1-го вида, 
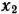изделий 2-го вида, 
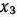изделий 3-го вида и 
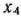изделий 4-го вида. Тогда задача состоит в определении максимального значения прибыли
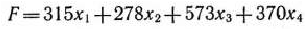
при ограничениях:
на имеющийся фонд рабочего времени каждой из групп оборудования:
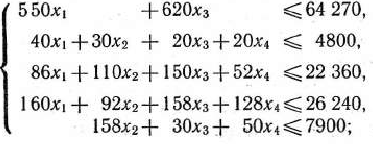
на возможное использование комплектующих изделий:
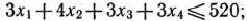
на возможный объем выполнения сборочно-наладочных работ
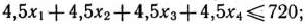
на возможный выпуск изделий каждого вида:
Перепишем теперь целевую функцию и систему ограничений нашей задачи в соответствии с требованиями ППП ЛП АСУ. Эти требования аналогичны требованиям, предъявляемым к записи задачи ППП ЛП2.
Присвоим переменным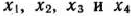 
соответственно имена ПР1, ПР2, ПРЗ и ПР4, ограничениям (45) — имена ТОКАР, ФРЕЗЕР, СВЕРЛИЛ, РАСТОЧ и ШЛИФОВАЛ, ограничениям (46) и (47) — имена КОМПЛЕКТ и СБОРКА, а целевой функции (44) — имя ПРИБ.
С учетом введенных имен целевую функцию задачи и ограничения (45) — (47) запишем в виде следующей системы уравнений:
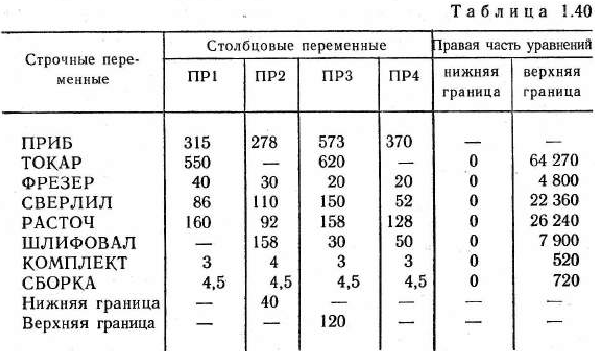
Используя полученные уравнения и учитывая значения правых частей ограничений (строчные переменные) и граничные условия на столбцовые переменные, составим матрицу исходных данных задачи (табл. 1.40).
На основе табл. 1.40 исходные данные запишем на бланке для последующей перфорации. При этом используем разбиение бланка на вспомогательные поля аналогично требованиям, предъявляемым ППП ЛП2. Однако исходные данные из табл. 1.40 переносим на бланк в «секционном» формате.
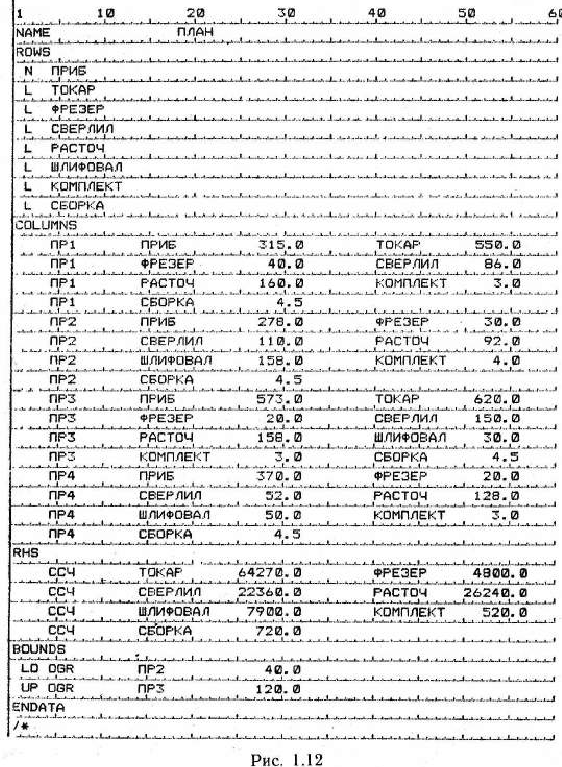
Запись исходных данных на бланке начинается словом NAME и заканчивается словом ENDATA (рис. 1.12).
Слово NAME записываем с позиции 1, а с позиции 15 записываем имя, присваиваемое задаче, которое должно содержать не более восьми буквенно-цифровых символов.
Слово ENDATA записываем с позиции 1 после окончания записи исходных данных. Между словами ENDATA и NAME записываем в виде пяти секций условия задачи:
1) секция строк (имен ограничений) — ROWS;
2) секция столбцов (элементов матрицы)—COLUMNS;
3) секция свободных членов ограничений — RHS;
4) секция интервалов — RANGES;
5) секция границ переменных — BOUNDS.
В секциях ROWS указываем строчные переменные; поле I — тип ограничения, поле 2— имя переменной (см. рис. 1.14). Для обозначения типа переменной используются:
L — переменная, ограниченная сверху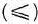 
G — переменная, ограниченная снизу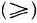 
;
Е — фиксированная переменная (=);
N — неограниченная переменная (от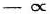
до 
).
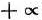В секции COLUMNS записываем элементы табл. 1.40 аналогично тому, как это было сделано при записи исходных данных задачи с использованием ППП ЛП2 (рис. 1.12).
Секция RHS содержит ненулевые значения свободных членов системы ограничений задачи. Каждый свободный член записываем вместе с именем столбца свободных членов и именем тон строки, которой он соответствует.
Секция RANGES не является обязательной. Она используется лишь тогда, когда для строчных переменных имеются двусторонние ограничения. В этом случае в секции RANGES указываются разности между верхними и нижними пределами изменения переменных, т.е. интервалы их изменений. При этом в поле 2 указывается имя набора интервалов, в полях 3 и 5
записывается имя переменных, в полях 4 и 6 помещаются величины интервалов. В рассматриваемой задаче данная секция не используется.
В секции BOUNDS, которая также не является обязательной, указываются верхние и нижние границы для столбцовых переменных. Эти границы записываются аналогично тому, как это было сделано для граничных условий при использовании ППП ЛП2. Для того чтобы указать тип ограничения, используются следующие обозначения:
UP — переменная, ограниченная сверху ;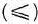
LO—переменная, ограниченная снизу ;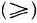
FX — фиксированная переменная ( = );
FR — неограниченная переменная (от 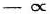до :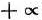
MI — переменная с бесконечной нижней границей .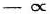
Тип ограничения указывается в поле 1.В поле 2 записывается имя набора граничных условий, в поле 3 — имя переменной, а в поле 4 — значение границ (см. рис. 1.14).
Имена переменных в секции BOUNDS записываются в такой же последовательности, в какой они записаны в секции COLUMNS.
Секция BOUNDS не является обязательной. Если границы неременных не определены, то они автоматически устанавливаются как 0 и ос.
Чтобы теперь получить программу решения задачи, определяем операторы управления заданиями ОС ЕС, управляющие операторы ПППЛПАСУ и исходные данные. Управляющую программу решения задачи записываем на стандартном бланке начиная с позиции 10 (рис. 1.13).
Начало управляющей программы определяет оператор PROGRAM. Микрооператор INIT1ALZ осуществляет инициализацию пакета (определяет начальные значения для ряда параметров, значений, допусков и т. п.).
Управляющие операторы MOVE устанавливают обязательные параметры задачи:
MOVE (XDATA, ‘ПЛАН’) — имя входных данных;
MOVE (XPBNAME, ‘OPTIM’) — имя, присваиваемое решаемой задаче.
Первое имя совпадает с именем, указанным при записи исходных данных задачи на бланке, а под вторым будет создана задача на проблемном файле.
Благодаря указанию процедуры CONVERT будут считаны входные данные под именем ПЛАН, преобразованы в двоичный формат и записаны на проблемном файле под именем OPTIM. Наличие параметра SUMMARY в процедуре CONVERT после обработки входных данных обеспечит распечатку краткой статистической информации о строках и столбцах исходной матрицы.
Наличие последующей процедуры BCDOUT обеспечивает распечатку на АЦПУ входных данных задачи в том же порядке и формате, в каком были сведены секции входных данных.
Параметры процедуры SETUP указывают на то, что задача должна быть решена на максимум (если на минимум, то вместо МАХ указывается MIN), далее, что существует секция BOUNDS с именем строки ограничений на переменные OGR (если бы в задаче была секция RANGES, то были бы указаны имя этой секции и имя столбца интервалов).
Следующие два оператора MOVE устанавливают имя целевой функции (ПРИБ) и имя столбца свободных членов (ССЧ), а благодаря указанию XGUARDPF-1 обеспечивается защита проблемного файла.
Микрокоманда OPTIMIZE используется для получения оптимального решения, а процедура SOLUTION выводит его на печать. Вместо микрокоманды OPTIMIZE может быть использована процедура PRIMAL.
В конце управляющей программы указываются два оператора: EXIT и PEND. Их наличие является обязательным. Первый оператор возвращает управление операционной системе ОС ЕС, а оператор PEND указывает на конец управляющей программы.
По итогам решения задачи выводится стандартный отчет об оптимальном решении (табл. 1.41). Этот отчет состоит из двух частей: СЕКЦИИ 1 — СТРОКИ, в которой приводится соответствующая информация о строчных переменных, и СЕКЦИИ 2 — СТОЛБЦЫ, в которой содержится информация о столбцовых переменных.
В СЕКЦИИ 1 в столбце «Тип» указывается, какое значение приняла данная строчная переменная в оптимальном плане задачи. При этом употребляются следующие обозначения:
** —значение переменной является недопустимым;
BS — переменная является базисной и приняла свое значение из интервала возможного изменения;
FQ — переменная имеет фиксированное значение;
UL — переменная приняла свое верхнее значение;
LL — переменная приняла свое нижнее значение;
FR — переменная является небазисной и приняла некоторое произвольное значение.
В столбце «Решение» указывается значение строчной переменной, которое она принимает при оптимальном плане задачи, т. е. величина используемого ресурса, а в столбце «Дополнительная переменная» — объемы неиспользуемых ресурсов. Так, из табл. 1.41 видно, что останутся неиспользованными 150 комплектующих изделий, сверлильное и расточное оборудование будет свободным соответственно 5262 и 4380 человеко-ч, а на сборочно-наладочных работах простои составят 22,5 человеко-ч.
Следующие два столбца СЕКЦИИ 1 «Нижняя граница» и «Верхняя граница» характеризуют интервалы возможных изменений строчных переменных, а столбец «Оценка строки» определяет двойственные оценки соответствующих переменных. Заметим, что знаки оценок строки соответствуют тому случаю, когда находится минимум целевой функции. Если находится максимум функции, как в данном случае, то необходимо заменить эти знаки на противоположные.
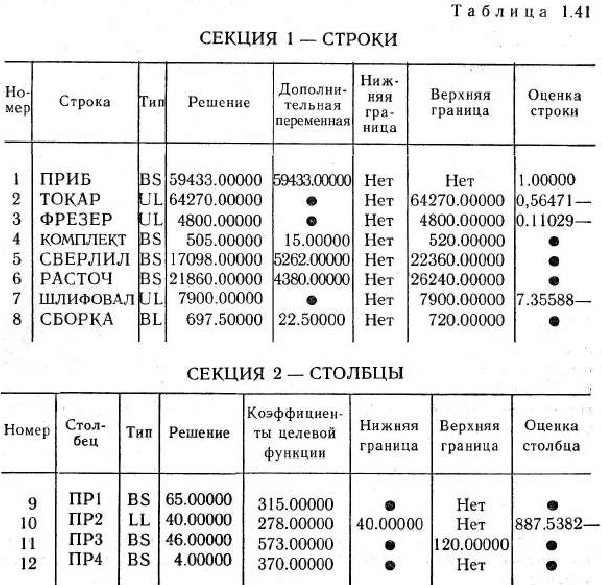
СЕКЦИЯ 2 — СТОЛБЦЫ содержит информацию о столбцовых переменных. Из столбца «Решение» видим, что оптимальным планом производства продукции является план, согласно которому изготовляется 65 изделий 1-го вида, 40 изделий 2-го вида, 63 изделия 3-го вида и 4 изделия 4-го вида. В соответствии с этим планом прибыль от реализации производимой продукции равна 59 433 руб.
| Графическое решение задач линейного программирования |
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
