Задача 1.30.
Найти максимальное значение функции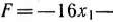 
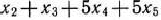при условиях
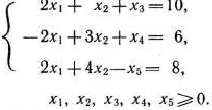
Решение:
В отличие от рассмотренных выше задач в исходной задаче ограничения заданы в виде уравнений. При этом число неизвестных равно пяти. Поэтому данную задачу следует свести к задаче, в которой число неизвестных было бы равно двум. В рассматриваемом случае это можно сделать путем перехода от исходной задачи, записанной в форме основной, к задаче, записанной в форме стандартной.
Выше было показано (см. § 1.2), что исходная задача записана в форме основной для задачи, состоящей в нахождении максимального значения функции
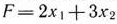
при условиях
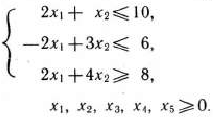
Из целевой функции исходной задачи переменные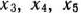 
исключены с помощью подстановки их значений из соответствующих уравнении системы ограничений.
Построим многоугольник решений полученной задачи (рис. 1.7). Как видно из рис. 1.7, максимальное значение целевая функция задачи принимает в точке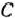 
пересечения прямых I и II. Вдоль каждой из граничных прямых значение одной из переменных, исключенной при переходе к соответствующему неравенству, равно нулю. Поэтому в каждой из вершин полученного многоугольника решений последней задачи по крайней мере две переменные исходной задачи принимают нулевые значения. Так, в точке 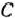имеем 
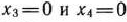. Подставляя эти значения в первое и второе уравнения системы ограничений исходной задачи, получаем систему двух уравнений
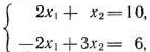
решая которую находим
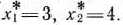
Подставляя найденные значения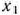 
и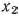 
в третье уравнение системы ограничений исходной задачи, определяем значение переменной 
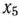, равное 14.
Следовательно, оптимальным планом рассматриваемой задачи является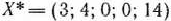 
. При этом плане значение целевой функции есть 
.
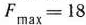Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
