Оглавление:
Теорема об изменении количества движения
Количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость mv.
Вектор количества движения совпадает по направлению с вектором скорости. Единица измерения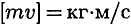 
.
Произведение постоянного вектора силы на некоторый промежуток времени, в течение которого действует эта сила, называется импульсом силы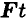 
.
Вектор импульса силы по направлению совпадает с вектором сила
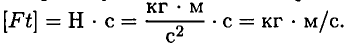
Использовав основное уравнение динамики, после преобразования можно получить соотношение между количеством движения и импульсом силы (рис. 17.1).
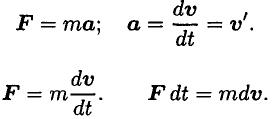
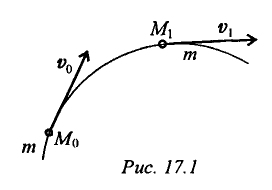
Проинтегрируем обе части равенства:
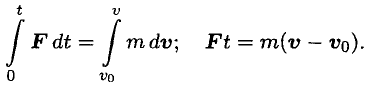
Полученное соотношение выражает теорему об изменении количества движения точки:
Изменение количества движения точки за некоторый промежуток времени равно импульсу силы, действующему на точку в течение того же промежутка времени.
Теорема об изменении кинетической энергии
Энергией называется способность тела совершать механическую работу.
Существуют две формы механической энергии: потенциальная энергия, или энергия положения, и кинетическая энергия, или энергия движения.
Потенциальная энергия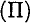 
определяет способность тела совершать работу при опускании с некоторой высоты до уровня моря. Потенциальная энергия численно равна работе силы тяжести.
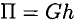, где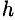 
— высота точки над уровнем моря.
Кинетическая энергия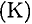 
определяется способностью движущегося тела совершать работу. Для материальной точки кинетическая энергия рассчитывается по формуле
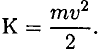
Кинетическая энергия — величина скалярная, положительная.
Единицы измерения:
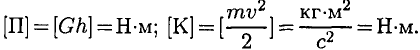
нергия имеет размерность работы.
Запишем для материальной точки (рис. 17.2) основное уравнение движения
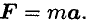
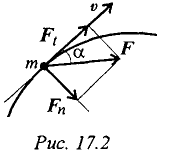
Спроектируем обе части векторного равенства на направление скорости:
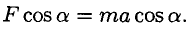
Известно, что
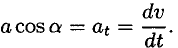
Откуда
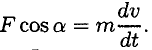
Умножив обе части полученного выражения на некоторое перемещение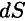 
, получим:
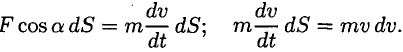
Интегрируем обе части равенства
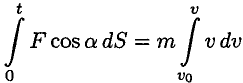
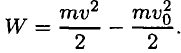
Полученное равенство выражает теорему об изменении кинетической энергии точки:
Изменение кинетической энергии на некотором пути равно работе всех действующих па точку сил на том же пути.
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:
| Мощность |
| Коэффициент полезного действия |
| Основы динамики системы материальных точек |
| Основные требования к деталям и конструкциям и виды расчетов в сопротивлении материалов |
