Пересечение линии с поверхностью
В общем случае для графического определения положения точек пересечения линии с поверхностью необходимо выполнить ряд геометрических построений в следующей последовательности: заключить линию во вспомогательную поверхность; определить линию пересечения этой поверхности с заданной поверхностью; отметить точки пересечения построенной линии с заданной.
Этот алгоритм является универсальным, пригодным для решения любых задач. Ранее (лекция 4, рис. 4.5 и 4.6) он применялся для построения проекций точки пересечения прямой с плоскостью, где в качестве вспомогательной секущей поверхности использовалась плоскость и строилась прямая линии пересечения ее с заданной плоскостью, а искомая проекция точки пересечения определялась как место пересечения этой линии с заданной прямой.
На рис. 12.1-12.3 проиллюстрирован тот же алгоритм применительно к построению точки пересечения кривой линии 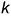 с плоскостью
с плоскостью 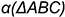 . В качестве секущей поверхности в данном случае следует использовать проецирующую цилиндрическую поверхность, в частности, горизонтально-проецирующую
. В качестве секущей поверхности в данном случае следует использовать проецирующую цилиндрическую поверхность, в частности, горизонтально-проецирующую 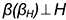 , в которую должна быть заключена кривая
, в которую должна быть заключена кривая 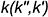 . Для этого на чертеже (рис. 13.3) обозначаем горизонтальный след этой поверхности
. Для этого на чертеже (рис. 13.3) обозначаем горизонтальный след этой поверхности 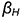 — Горизонтальная проекция линии ее пересечения с заданной плоскостью
— Горизонтальная проекция линии ее пересечения с заданной плоскостью 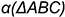 совпадает с ним, располагаясь между точками
совпадает с ним, располагаясь между точками 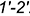 .
.
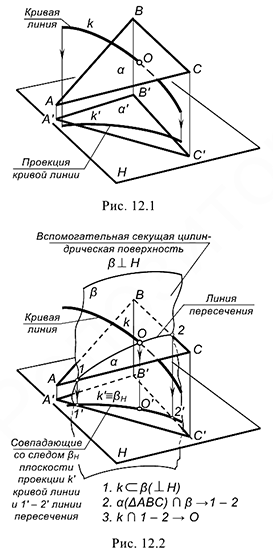
Для построения ее фронтальной проекции воспользуемся произвольными вспомогательными прямыми линиями, принадлежащими плоскости. Вначале задаем их горизонтальные проекции, например, через вершину  . Затем по
. Затем по
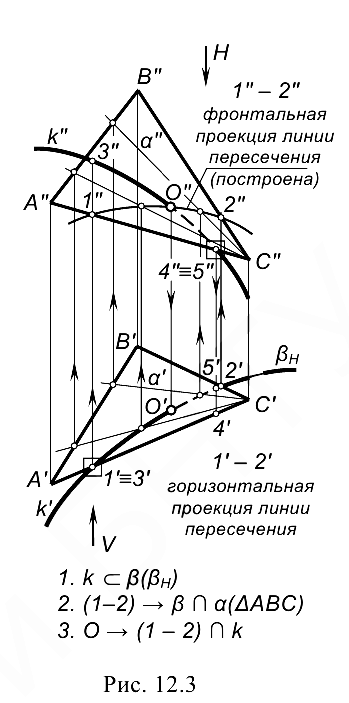
точкам их пересечения со стороной 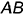 находим фронтальные проекции вспомогательных прямых и определяем на них фронтальные проекции точек пересечения с ними заданной кривой. Проводим через найденные точки плавную кривую линию, являющуюся, таким образом, фронтальной проекцией линии пересечения, и отмечаем на ней место пересечения с фронтальной проекцией заданной кривой
находим фронтальные проекции вспомогательных прямых и определяем на них фронтальные проекции точек пересечения с ними заданной кривой. Проводим через найденные точки плавную кривую линию, являющуюся, таким образом, фронтальной проекцией линии пересечения, и отмечаем на ней место пересечения с фронтальной проекцией заданной кривой 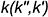 — точку
— точку 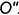 . Это и будет фронтальная проекция искомой точки пересечения заданной кривой
. Это и будет фронтальная проекция искомой точки пересечения заданной кривой 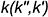 с плоскостью
с плоскостью 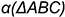 . Затем, воспользовавшись линией связи, находим горизонтальную проекцию
. Затем, воспользовавшись линией связи, находим горизонтальную проекцию 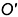 точки пересечения.
точки пересечения.
Этот алгоритм применен и для построения точек пересечения прямой линии с поверхностями геометрических тел — призмы, пирамиды и самопересекающегося тора (рис. 12.8, а, б, в). Поскольку поверхности этих тел являются замкнутыми, то необходимо найти по две точки пересечения на каждой из них.
При пересечении с призмой (рис. 12.8, а) в качестве секущей плоскости для заключения в нее заданной прямой 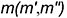 использовалась фронтально-проецирующая плоскость
использовалась фронтально-проецирующая плоскость 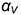 При пересечении с пирамидой (рис. 12.8, б) в качестве секущей плоскости для заключения в нее заданной прямой
При пересечении с пирамидой (рис. 12.8, б) в качестве секущей плоскости для заключения в нее заданной прямой 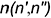 использовалась горизонтально-проецирующая плоскость Он- При пересечении с самопересекающимся тором (рис. 12.8, в) в качестве секущей плоскости для заключения в нее заданной прямой
использовалась горизонтально-проецирующая плоскость Он- При пересечении с самопересекающимся тором (рис. 12.8, в) в качестве секущей плоскости для заключения в нее заданной прямой 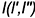 использовалась фронтальная плоскость
использовалась фронтальная плоскость 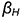 . Далее все действия аналогичны рассмотренным. В каждом случае вначале строилась линия пересечения поверхности плоскостью, исходя из ее проецирующего положения, определялись на ней точки пересечения с заданной прямой, а при окончательном оформлении — видимость на чертеже.
. Далее все действия аналогичны рассмотренным. В каждом случае вначале строилась линия пересечения поверхности плоскостью, исходя из ее проецирующего положения, определялись на ней точки пересечения с заданной прямой, а при окончательном оформлении — видимость на чертеже.
В качестве секущей плоскости при определении точек пересечения прямой с поверхностью могут использоваться также плоскости общего положения, пересекающие поверхность вдоль ее образующих (рис. 12.8, г, д). Так, для построения точек пересечения прямой 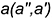 общего положения с поверхностью прямого кругового конуса (рис. 12.8, г) показано использование плоскости общего положения а, проходящей через вершину конуса и заданную прямую. Плоскость задана двумя пересекающимися прямыми. Одна из них — это заданная прямая
общего положения с поверхностью прямого кругового конуса (рис. 12.8, г) показано использование плоскости общего положения а, проходящей через вершину конуса и заданную прямую. Плоскость задана двумя пересекающимися прямыми. Одна из них — это заданная прямая 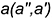 , вторая — пересекающаяся с ней произвольная прямая
, вторая — пересекающаяся с ней произвольная прямая 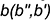 , проходящая через вершину конуса. Для построения проекций образующих, вдоль которых плоскость пересекает поверхность конуса, найден ее горизонтальный след, затем проекции
, проходящая через вершину конуса. Для построения проекций образующих, вдоль которых плоскость пересекает поверхность конуса, найден ее горизонтальный след, затем проекции 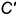 и
и 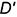 точек его пересечения с горизонтальным следом основания конуса и фронтальные проекции
точек его пересечения с горизонтальным следом основания конуса и фронтальные проекции 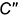 и
и 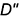 этих точек. Искомые проекции точек
этих точек. Искомые проекции точек 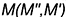 и
и 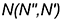 пересечения заданной прямой общего положения с поверхностью конуса находятся в местах пересечения с ней построенных образующих.
пересечения заданной прямой общего положения с поверхностью конуса находятся в местах пересечения с ней построенных образующих.
Аналогичные действия выполнены и для построения проекций 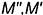 и
и 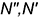 точек пересечения прямой общего положения
точек пересечения прямой общего положения 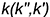 с поверхностью наклонного эллиптического цилиндра (рис. 12.8, г)). Для этого использовалось задание плоскости общего положения
с поверхностью наклонного эллиптического цилиндра (рис. 12.8, г)). Для этого использовалось задание плоскости общего положения 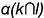 также двумя пересекающимися прямыми, одна из которых, как и в предыдущем случае, — это заданная прямая
также двумя пересекающимися прямыми, одна из которых, как и в предыдущем случае, — это заданная прямая 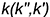 а пересекающаяся с ней в произвольной точке
а пересекающаяся с ней в произвольной точке 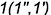 вторая прямая линия — это прямая
вторая прямая линия — это прямая 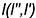 , параллельная образующим цилиндра.
, параллельная образующим цилиндра.
Строился горизонтальный след этой плоскости и по точкам пересечения его с горизонтальным следом заданного цилиндра находились образующие, по которым вспомогательная плоскость общего положения 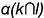 пересекает цилиндр. В местах пересечения с проекциями этих образующих проекций прямой общего положения
пересекает цилиндр. В местах пересечения с проекциями этих образующих проекций прямой общего положения 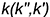 находятся искомые проекции
находятся искомые проекции 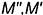 и
и 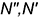 точек пересечения заданной прямой с поверхностью цилиндра.
точек пересечения заданной прямой с поверхностью цилиндра.
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Цилиндрические и конические винтовые линии |
| Кривые поверхности |
| Касательные плоскости и нормаль к поверхности |
| Метод проекций. Образование чертежа по Монжу. Проекции точки |

