Кривые линии и поверхности
Общие сведения о кривых линиях: определения, классификация, термины
Кривую линию можно представить как траекторию движущейся точки в пространстве [12]. Примером служат, например, спираль Архимеда, цилиндрическая или коническая винтовая линия (рис. 11.7, а и б и рис. 11.8, а).
Кривая линия может быть получена в результате пересечения поверхностей между собой или пересечения кривой поверхности плоскостью. На поверхности конуса в зависимости от положения секущей плоскости образуется ряд кривых линий — эллипс, гипербола, парабола, окружность (см. рис. 7.11-7.15). Эллипс или окружность получаются также в сечениях плоскостью цилиндра (см. рис. 7.7 и 7.8) и кругового однополостного гиперболоида. Осевыми сечениями однополостного гиперболоида являются гиперболы (см. рис. 7.29, й), а параболоида — параболы (см. рис. 7.29, а).
Кривые линии могут быть плоскими и пространственными (линиями двоякой кривизны). Примерами плоских кривых линий являются окружность, эллипс, парабола, спираль Архимеда, пространственных — винтовые линии, линии пересечения кривых поверхностей.
Пространственная линия всегда проецируется в виде кривой, а плоская — только при условии, что ее плоскость не перпендикулярна плоскости проекций (если перпендикулярна — проецируются в виде прямой).
Линия считается закономерной, если в своем образовании она подчинена какому-либо геометрическому закону, а если при этом она определяется в декартовых координатах алгебраическим уравнением, ее называют алгебраической. Степень уравнения определяет «порядок» кривой. Так, например, эллипс — кривая второго порядка. Проекция кривой сохраняет ее порядок или оказывается кривой более низкого порядка.
Если кривая не определяется алгебраическим уравнением, то она относится к числу трансцендентных.
Касательная прямая к кривой линии в общем случае проецируется в виде касательной к проекции этой кривой. Так, например, касательная к окружности в некоторой точке проецируется в касательную к эллипсу, являющемуся проекцией этой окружности.
Если в каждой точке кривой можно построить только одну касательную прямую линию, то кривая называется плавной или монотонной.
Такая плоская кривая в каждой ее точке имеет только одну нормаль -прямую, перпендикулярную к соответствующей касательной в каждой точке кривой и принадлежащую плоскости.
Составные кривые линии — классификация точек стыка
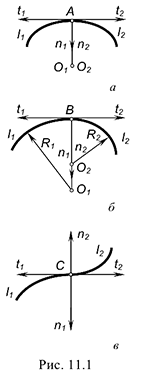
Кривая линия может быть составной, если на ней есть точка стыка, называемая вершиной, в которой соединяются две кривые линии (рис. 11.1 и 11.2) [23]. Существует понятие обыкновенная вершина кривой. Это точка  на рис. 11.1. В ней соединяются (соприкасаются) две монотонные плоские кривые линии
на рис. 11.1. В ней соединяются (соприкасаются) две монотонные плоские кривые линии  и
и 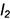 , касательные
, касательные 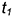 и
и 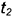 к которым в этой точке противоположно направлены по одной линии, а нормали
к которым в этой точке противоположно направлены по одной линии, а нормали 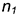 и
и 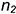 и центры кривизны
и центры кривизны 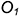 и
и 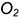 совпадают (рис. 11.1, а).
совпадают (рис. 11.1, а).
Если хотя бы одно из указанных условий не выполняется, то речь ведут об особой точке на составной кривой. Двойной называют особую точку 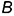 стыка (вершину) составной кривой, если касательные направлены в разные стороны, нормали совпадают по направлению, а вот центры кривизны различны (рис. 11.1, б). Точка перегиба получается в том случае, когда в ней противоположные направления имеют и касательные, и нормали к составной кривой. Это особая точка стыка
стыка (вершину) составной кривой, если касательные направлены в разные стороны, нормали совпадают по направлению, а вот центры кривизны различны (рис. 11.1, б). Точка перегиба получается в том случае, когда в ней противоположные направления имеют и касательные, и нормали к составной кривой. Это особая точка стыка 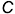 (рис. 11.1, в).
(рис. 11.1, в).
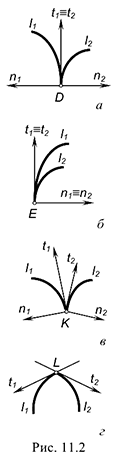
Из всего многообразия точек стыка следует уделить внимание и так называемым точкам возврата 1-го и 2-го рода и точке излома (рис. 11.2) [23].
На рис. 11.2, а изображена точка 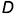 возврата 1-го рода, в которой касательные
возврата 1-го рода, в которой касательные 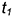 и
и 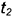 к каждой кривой совпадают по направлению, а нормали
к каждой кривой совпадают по направлению, а нормали 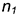 и
и 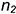 имеют противоположные направления.
имеют противоположные направления.
На рис. 11.2, б изображена точка 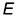 возврата 2-го рода, в которой и касательные
возврата 2-го рода, в которой и касательные 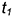 и
и 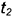 к каждой кривой, и нормали
к каждой кривой, и нормали 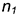 и
и 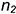 попарно совпадают по направлению.
попарно совпадают по направлению.
На рис. 11.2, в и г изображены точки 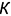 и
и  излома, в которых касательные
излома, в которых касательные 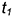 и
и 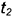 не принадлежат одной прямой.
не принадлежат одной прямой.
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Косоугольная (фронтальная) диметрия |
| Примеры построения аксонометрических проекций |
| Цилиндрические и конические винтовые линии |
| Плоские и пространственные кривые линии |

