Оглавление:
Примеры построения аксонометрических проекций
На рис. 10.6 показан пример построения аксонометрической проекции правильной треугольной пирамиды со срезом фронтально-проецирующей плоскостью 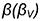 в прямоугольной диметрии.
в прямоугольной диметрии.
Построение аксонометрии пирамиды выполняется по предлагаемому графическому алгоритму
1-е действие. Отнести пирамиду к системе прямоугольных координат  ,
,  и
и 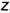 , оси которой параллельны осям натуральной системы координат, но проходят через высоту пирамиды (ось
, оси которой параллельны осям натуральной системы координат, но проходят через высоту пирамиды (ось 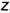 ) и ее основание (оси
) и ее основание (оси 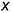 и
и 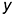 ).
).
2-е действие. Определить в принятой системе координат на проекциях пирамиды координаты 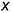 ,
, 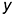 и
и 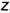 отмеченных точек 1, 2, 3, лежащих на ребрах пирамиды, и точек
отмеченных точек 1, 2, 3, лежащих на ребрах пирамиды, и точек  — вершин основания пирамиды.
— вершин основания пирамиды.
3-е действие. На свободном поле чертежа провести аксонометрические оси прямоугольной диметрии из произвольной точки 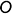 : ось
: ось 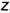 — вертикально, ось
— вертикально, ось 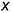 — под углом
— под углом 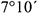 , а ось
, а ось 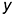 — под углом
— под углом 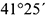 к горизонтальной линии (использовать графический способ построения аксонометрических осей).
к горизонтальной линии (использовать графический способ построения аксонометрических осей).
4-е действие. Построить тонкими линиями аксонометрическую проекцию пирамиды без среза.
4.1. Построить аксонометрическое изображение основания пирамиды 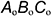 по координатным ломаным этих точек (основание лежит в системе осей
по координатным ломаным этих точек (основание лежит в системе осей 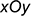 и называется вторичной проекцией):
и называется вторичной проекцией):
- точка
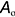 : координатная ломаная
: координатная ломаная  ;
; - точка
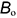 : координатная ломаная
: координатная ломаная 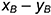 ,
, - точка
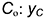 .
.
!!! Координатные отрезки параллельны соответствующим аксонометрическим осям.
4.2. Построить по координате 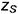 на аксонометрической оси
на аксонометрической оси 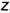 проекцию вершины пирамиды и соединить вершину
проекцию вершины пирамиды и соединить вершину 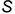 с точками основания
с точками основания 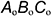 ребрами, то есть построить аксонометрию пирамиды.
ребрами, то есть построить аксонометрию пирамиды.
5-е действие. Достроить срез на аксонометрии пирамиды, построив на ребрах пирамиды по координатам 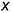 ,
, 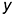 и
и 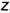 аксонометрические проекции отмеченных точек 1, 2 и 3 по соответствующим плоским координатным ломанным:
аксонометрические проекции отмеченных точек 1, 2 и 3 по соответствующим плоским координатным ломанным:
- точка 1 на ребре
 : координатная ломаная —
: координатная ломаная — 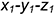
- точка 2 на ребре
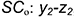 ;
; - точка 3 на ребре
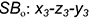 .
.
6-е действие. Оформить аксонометрию пирамиды, выполнив толстыми линиями ее видимый контур (оставить тонкими линиями полную проекцию пирамиды, невидимые линии и линии построения).
На рис. 10.7 показан пример построения аксонометрической проекции конуса со срезами двумя фронтально-проецирующими плоскостями (в сечении плоскостью 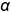 — треугольник со сторонами-образующими, в сечении плоскостью
— треугольник со сторонами-образующими, в сечении плоскостью 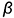 — эллипс) в прямоугольной изометрии.
— эллипс) в прямоугольной изометрии.
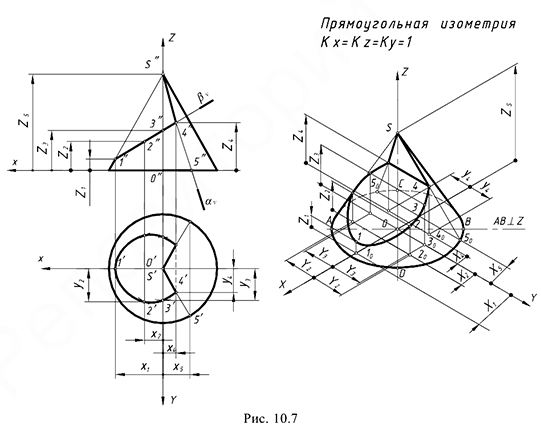
Графические действия для построения аксонометрии конуса соответствуют предложенному алгоритму для построения аксонометрии пирамиды:
1-е действие. Отнести конус к такой же системе прямоугольных координат 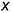 ,
, 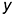 и
и 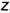 (ось
(ось 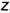 совпадет с высотой конуса, оси
совпадет с высотой конуса, оси 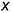 и
и 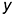 проходят по основанию конуса).
проходят по основанию конуса).
2-е действие. Определить координаты 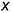 ,
, 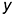 и
и 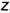 для точек 1, 2, 3 и 4 на поверхности конуса для построения сечений на его аксонометрии.
для точек 1, 2, 3 и 4 на поверхности конуса для построения сечений на его аксонометрии.
3-е действие. На свободном поле чертежа отметить точку 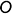 начала аксонометрических координат и провести оси прямоугольной изометрии под углами
начала аксонометрических координат и провести оси прямоугольной изометрии под углами 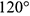 с вертикальной осью
с вертикальной осью 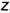 .
.
4-е действие. Построить аксонометрическую проекцию конуса без срезов:
4.1. Построить эллипс основания конуса с центром в точке 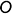 , большая ось которого перпендикулярна аксонометрической оси
, большая ось которого перпендикулярна аксонометрической оси 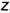 , так как окружность основания конуса лежит в горизонтальной плоскости (см. графическое построение овала 2 на рис. 10.3).
, так как окружность основания конуса лежит в горизонтальной плоскости (см. графическое построение овала 2 на рис. 10.3).
4.2. Построить вершину конуса точку 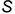 на оси
на оси 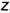 по ее координате
по ее координате 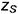 и провести две касательные к эллипсу через вершину
и провести две касательные к эллипсу через вершину 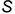 .
.
5-е действие. Достроить срезы на аксонометрии конуса, построив аксонометрические проекции отмеченных точек 1, 2, 3 и 4 по соответствующим плоским координатным ломаным:
- точка 1: координатная ломаная
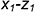 ;
; - точки 2: координатная ломаная
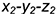
- точки 3: координатная ломаная
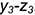 ;
; - точки 4: координатная ломаная
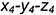 (лежат на образующих
(лежат на образующих 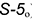 ).
).
Соединить построенные точки соответствующими линиям (участок эллипса и треугольник).
6-е действие. Оформить чертеж аксонометрии конуса, выполнив толстыми линиями ее видимый контур (оставить тонкими линиями полный контур пирамиды, невидимые линии и линии построения).
На рис. 10.8 показано построение аксонометрической проекции цилиндра с полуцилиндрическим вырезом (их радиусы равны) в прямоугольной изометрии.
В этом частном случае пересечения поверхностей для построения линии пересечения на профильной проекции следует применить теорему Г. Монжа, так как эти две цилиндрические поверхности 2-го порядка равных диаметров описаны вокруг сферы.
Построение аксонометрии выполняется по аналогичному графическому алгоритму
1-е действие. Отнести цилиндр к системе координатных осей 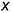 ,
, 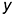 и
и 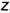 : оси
: оси 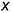 и
и 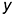 провести по нижнему основанию, а ось
провести по нижнему основанию, а ось 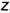 — по оси вращения цилиндра.
— по оси вращения цилиндра.
2-е действие. Обозначить характерные и промежуточные точки 1, 2, 3 и 4 на поверхности цилиндра и определить координаты 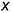 ,
, 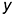 ,
, 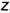 обозначенных точек для построения линии пересечения полуцилиндрического выреза с поверхностью заданного цилиндра (симметричные точки обозначены на одной половине окружности).
обозначенных точек для построения линии пересечения полуцилиндрического выреза с поверхностью заданного цилиндра (симметричные точки обозначены на одной половине окружности).
3-е действие. На свободном поле чертежа отметить точку 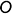 начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии: ось
начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии: ось 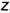 — вертикально, а оси
— вертикально, а оси 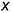 и
и 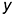 — под углами
— под углами 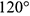 к оси
к оси 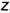 .
.
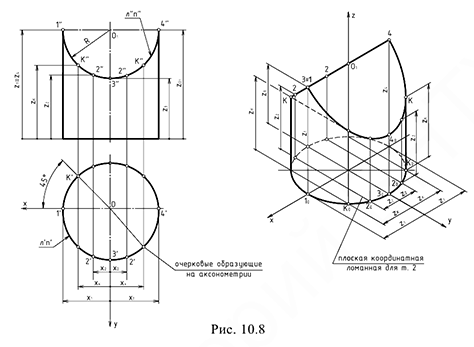
4-е действие. Построить аксонометрию цилиндра без выреза.
4.1. Построить эллипс нижнего основания цилиндра в точке 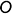 , большая ось которого перпендикулярна оси
, большая ось которого перпендикулярна оси 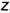 , так как окружность основания лежит в горизонтальной плоскости.
, так как окружность основания лежит в горизонтальной плоскости.
4.2. Построить точку 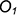 верхнего основания по координате
верхнего основания по координате 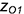 и эллипса верхнего основания; соединить эллипсы двумя очерковыми образующими по конечным точкам больших осей эллипсов.
и эллипса верхнего основания; соединить эллипсы двумя очерковыми образующими по конечным точкам больших осей эллипсов.
5-е действие. Достроить вырез на аксонометрии цилиндра, построив проекции обозначенных точек 1, 2, 3 и 4 по координатным ломаным (снизу вверх) 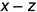 :
:
• точки 1 и 4 —> 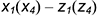 ;
;
• точки 2 —> 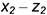 (четыре точки);
(четыре точки);
• точки 3 —> 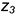 (две точки);
(две точки);
• точки 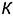 (на очерковых образующих; см. построения на горизонтальных проекциях) —>
(на очерковых образующих; см. построения на горизонтальных проекциях) —>  ;
;
• построенные точки соединить:
- одна плоская кривая проецируется на аксонометрию в виде эллипса;
- вторая плоская кривая проецируется в прямую линию (запомните!).
6-е действие. Соедините построенные точки соответствующими линиями — отрезками образующих и участками эллипсов.
7-е действие. Оформить аксонометрию цилиндра, выполнив толстыми линиями ее видимый контур (оставить тонкими линиями полный контур цилиндра, невидимые линии и линии построения).
На рис. 10.9 показан пример построения шара со срезами в прямоугольной изометрии.
Напомним, что сечением поверхности шара любой плоскостью является окружность. Но на чертеже окружности проецируются в эллипсы. В примере срезы выполнены профильной плоскостью  , горизонтальной плоскостью
, горизонтальной плоскостью 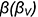 и фронтально-проецирующей плоскостью
и фронтально-проецирующей плоскостью 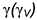 — Следовательно, на аксонометрическом изображении шара:
— Следовательно, на аксонометрическом изображении шара:
• эллипс окружности 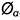 , лежащий в профильной плоскости;
, лежащий в профильной плоскости;
• эллипс окружности 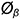 , лежащий в горизонтальной плоскости;
, лежащий в горизонтальной плоскости;
• эллипс как проекцию окружности, лежащий в плоскости 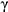 , по обозначенным точкам.
, по обозначенным точкам.
Аксонометрическим изображением шара в прямоугольной изометрии является окружность с диаметром, равным 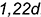 , где
, где 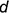 — диаметр шара.
— диаметр шара.
Графический алгоритм для построения аксонометрии шара следующий:
1-е действие. Отнести шар к системе координат 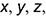 проходящих через его центр (точка
проходящих через его центр (точка 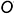 ).
).
2-е действие. Обозначить характерные точки 1, 2, 3, 4, 5 и б на поверхности шара и определить координаты обозначенных точек для построения срезов на аксонометрии.
3-е действие. На свободном поле чертежа отметить точку 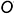 начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии.
начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии.
4-е действие. Построить аксонометрию шара без срезов — провести окружность диаметром 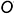 .
.
5-е действие. Достроить срезы на аксонометрии шара:
• построить эллипс диаметром 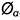 , большая ось которого перпендикулярна аксонометрической оси
, большая ось которого перпендикулярна аксонометрической оси 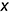 , с центром в точке
, с центром в точке 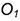 с координатой
с координатой 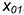 ;
;
• построить эллипс диаметром 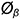 , большая ось которого перпендикулярна аксонометрической оси
, большая ось которого перпендикулярна аксонометрической оси 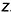 , с центром в точке
, с центром в точке 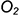 с координатой
с координатой 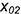 (построенные эллипсы пересекаются по линии 2-2);
(построенные эллипсы пересекаются по линии 2-2);
• построить по координате 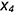 линию 4-4 на построенном горизонтальном эллипсе;
линию 4-4 на построенном горизонтальном эллипсе;
• построить по координатам точки 5 и 6: точку 5 — по ломаной 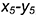 , а точку 6 — по координате
, а точку 6 — по координате 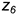 .
.
6-е действие. Соединить построенные точки 4-5-6 эллиптической кривой.
7-е действие. Оформить аксонометрию шара, выполнив толстыми линиями его видимый контур, оставив тонкими линиями полный очерк шара, невидимые линии и линии построения.
На рис. 10.10 показан пример построения половины открытого тора в прямоугольной изометрии.
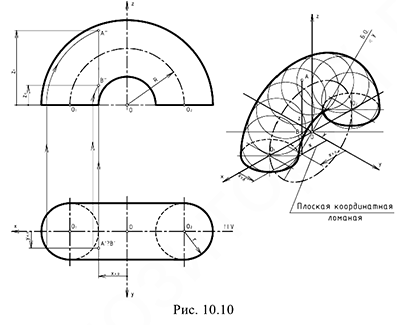
Построение аксонометрии выполняется по следующему графическому алгоритму
1-е действие. Отнести тор к системе координат 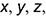 .
.
2-е действие. Если тор со срезами, обозначить характерный точки и определить их координаты: например, координаты точек 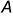 и
и 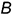 .
.
3-е действие. На свободном поле чертежа отметить точку 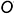 начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии.
начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии.
4-е действие. Построить эллипс направляющей окружности радиусом 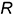 с центром в точке
с центром в точке 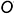 , большая ось которого перпендикулярна оси
, большая ось которого перпендикулярна оси 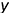 .
.
5-е действие. В полученных на оси 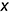 точках
точках 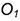 и
и 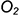 построить два эллипса образующих окружностей радиусом
построить два эллипса образующих окружностей радиусом 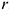 , большие оси которых перпендикулярны оси
, большие оси которых перпендикулярны оси 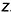 .
.
6-е действие. Построить аксонометрию тора:
• провести достаточное количество образующих окружностей диаметрами, равными 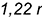 с центрами на эллипсе направляющей окружности тора;
с центрами на эллипсе направляющей окружности тора;
• провести две лекальные огибающие касательные кривые.
7-е действие. Достроить аксонометрические проекции заданных точек 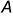 и
и 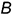 по их координатным ломаным:
по их координатным ломаным:
• точка 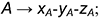
• точка 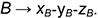
8-е действие. Оформить аксонометрию открытого тора.
На рис. 10.11 показан пример построения тороида (самопересекающегося тора) в прямоугольной изометрии.
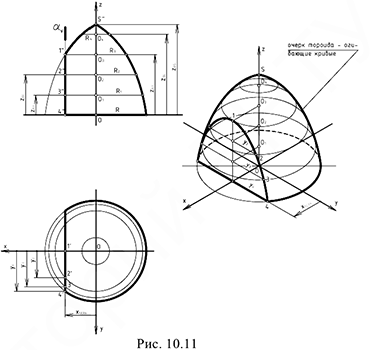
Построение аксонометрии выполняется по следующему графическому алгоритму
1-е действие. Отнести тор к системе координат 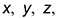 проходящей по его основанию и ось вращения.
проходящей по его основанию и ось вращения.
2-е действие. Рассечь тороид достаточным количеством плоскостей, перпендикулярных оси его вращения и определить радиус окружности каждого сечения (измерить линейкой) с центрами в точках 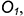
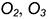 и т. д.
и т. д.
3-е действие. Обозначить характерные точки 1, 2, 3 и 4 среза и определить их координаты.
4-е действие. На свободном поле чертежа отметить точку 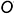 начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии.
начала аксонометрических координат и провести аксонометрические оси прямоугольной изометрии.
5-е действие. Построить аксонометрию тороида:
• построить семейство эллипсов в точках 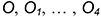 соответствующих радиусов
соответствующих радиусов 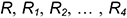 с координатами
с координатами 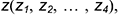 большие оси которых перпендикулярны оси
большие оси которых перпендикулярны оси 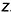 , так как лежат в горизонтальных плоскостях;
, так как лежат в горизонтальных плоскостях;
• построить точку 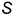 ;
;
• провести две касательные огибающие кривые к эллипсам.
6-е действие. Достроить срез на аксонометрии тороида по координатам отмеченных точек (построения см. рис. 10.11).
7-е действие. Оформить аксонометрию тороида.
!!! Аксонометрическая проекция глобоида в прямоугольной изометрии строится аналогично тем же способом «сечений».
На рис. 10.12 показан пример построения аксонометрической проекции правильной четырехгранной призмы со сквозным пазом, выполненным двумя профильными 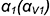 и
и 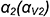 фронтально-проецирующей плоскостями
фронтально-проецирующей плоскостями 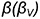 в косоугольной диметрии (коэффициенты искажения
в косоугольной диметрии (коэффициенты искажения 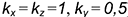 ).
).
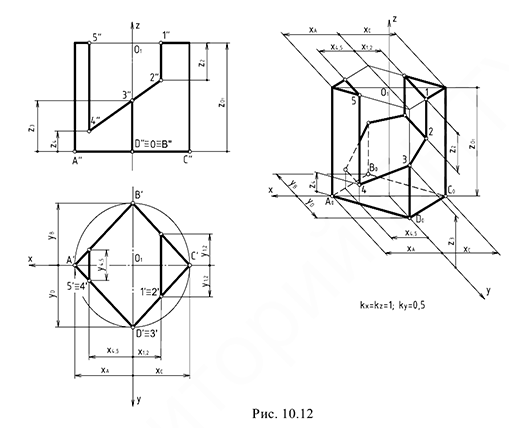
Построение аксонометрии призмы выполняется по следующему графическому алгоритму
1-е действие. Отнести («привязать») призму к системе прямоугольных координат 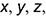 оси которой параллельны осям натуральной системы координат, относительно которой построены проекции призмы, но проходят через высоту призмы (ось
оси которой параллельны осям натуральной системы координат, относительно которой построены проекции призмы, но проходят через высоту призмы (ось 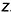 ) и через центр нижнего основания призмы (оси
) и через центр нижнего основания призмы (оси 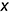 и
и 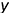 ).
).
2-е действие. Обозначить характерные точки 1, 2, …, 5 на поверхности призмы.
3-е действие. Определить в отнесенной к призме системе координат на ее проекциях координаты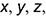 обозначенных точек:
обозначенных точек:
• точки 1 и 5, лежащих на верхнем основании и ребрах призмы;
• точек 2 и 4, лежащих на линиях пересечения плоскостей паза, а также обозначенных буквами 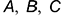 и
и  вершин нижнего основания призмы.
вершин нижнего основания призмы.
4-е действие. На свободном поле чертежа отметить точку О начала аксонометрических координат и провести аксонометрические оси косоугольной диметрии: ось 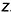 — вертикально; ось
— вертикально; ось 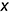 — горизонтально; ось
— горизонтально; ось 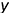 -под углом
-под углом 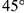 к горизонтальной линии (оси
к горизонтальной линии (оси 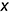 ).
).
5-е действие. Построить тонкими линиями аксонометрическую проекцию призмы без выреза:
5.1. Построить нижнее основание призмы 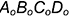 по координатам
по координатам 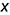 и
и 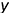 этих точек (основание лежит в горизонтальной плоскости с осями
этих точек (основание лежит в горизонтальной плоскости с осями 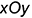 и называется вторичной проекцией):
и называется вторичной проекцией):
• точки 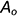 и
и 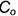 — симметрично по равным координатам
— симметрично по равным координатам 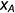 и
и 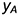 на оси
на оси 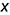 ;
;
• точки 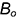 и
и 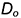 — по координатам
— по координатам 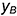 и
и 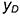 на оси
на оси 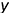 (координаты уменьшить в 2 раза!);
(координаты уменьшить в 2 раза!);
• соединить построенные вершины отрезками прямых линий.
5.2. Построить верхнее основание призмы:
• отложить от точки 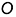 вверх координату
вверх координату 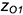 , равную высоте призмы, и через полученную проекцию точки
, равную высоте призмы, и через полученную проекцию точки 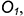 провести аксонометрические оси;
провести аксонометрические оси;
• из точек 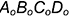 нижнего основания провести вертикально ребра призмы параллельно оси
нижнего основания провести вертикально ребра призмы параллельно оси 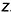 до пересечения с аксонометрическими верхнего основания и достроить верхнее основание призмы.
до пересечения с аксонометрическими верхнего основания и достроить верхнее основание призмы.
6-е действие. Достроить на аксонометрии призмы вырез по координатам обозначенных точек (сверху вниз):
• точки 1 и 5 на верхнем основании по координатам 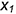 и
и 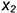 ;
;
• точки 2 и 4 — на вертикальных линиях, параллельных оси 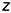 , по координатам
, по координатам 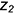 и
и 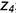 ;
;
• точки 3- на ребрах 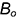 и
и 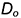 по координате
по координате 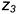 ;
;
7-е действие. Соединить построенные точки отрезками прямых линий.
8-е действие. Оформить аксонометрию призмы, выполнив толстыми линиями ее видимый контур; оставить тонкими линиями полную проекцию призмы, невидимые линии и линии построения.
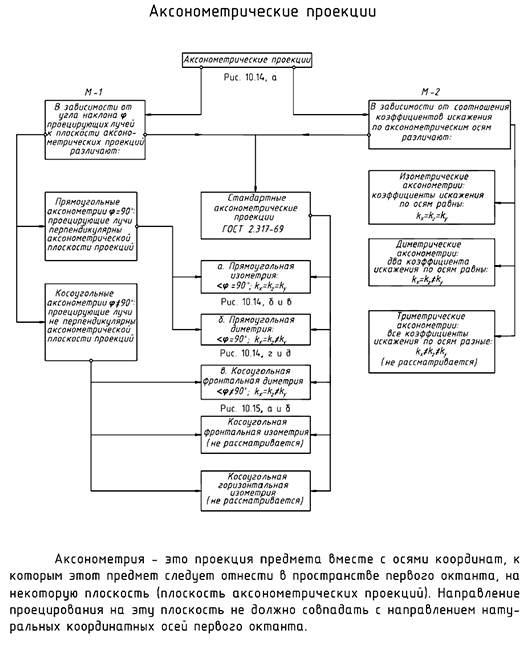
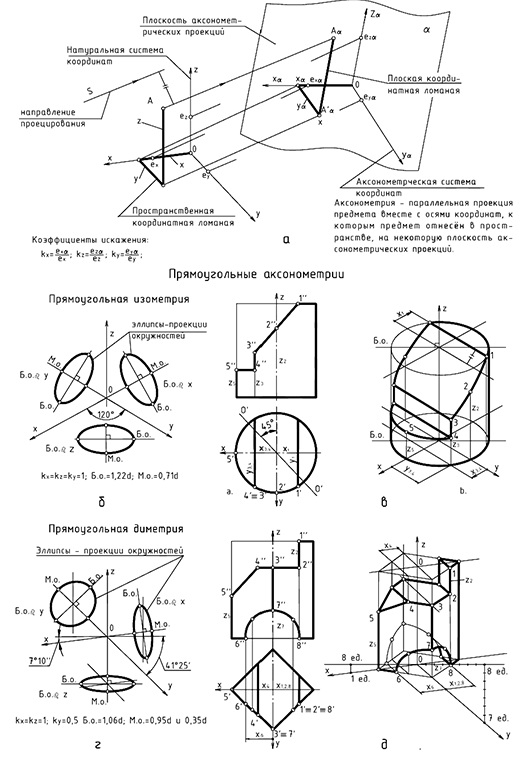
Структуризация материала десятой лекции в рассмотренном объеме схематически представлена на рис. 10.13 (лист 1). На последующих листах 2 и 3 компактно приведены иллюстрации к этой схеме для визуального закрепления основной части изученного материала при повторении (рис. 10.14 и 10.15).
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Прямоугольная диметрия |
| Косоугольная (фронтальная) диметрия |
| Кривые линии и поверхности |
| Плоские и пространственные кривые линии |

