Построение проекций призмы со срезами плоскостями частного положения
На рис. 7.3 показан пример построения проекций прямой правильной треугольной призмы высотой 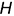 со срезами, выполненными плоскостями частного положения — фронтально-проецирующей плоскостью
со срезами, выполненными плоскостями частного положения — фронтально-проецирующей плоскостью 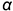 и профильной плоскостью
и профильной плоскостью 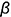 . Для упрощения графических описаний взята призма без срезов из предыдущего примера (см. рис. 7.1), горизонтальная, фронтальная и профильная проекции которой уже построены.
. Для упрощения графических описаний взята призма без срезов из предыдущего примера (см. рис. 7.1), горизонтальная, фронтальная и профильная проекции которой уже построены.
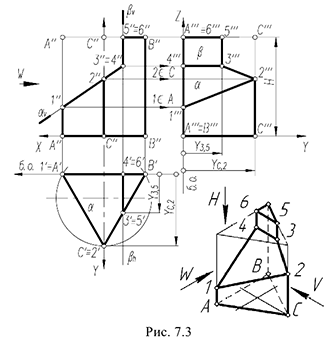
Для построения проекций призмы со срезами следует выполнить предлагаемый графический алгоритм, определяющий порядок действий при решении всех подобных задач:
1-е действие. Построить тонкими линиями на поле чертежа горизонтальную, фронтальную и профильную проекции заданной прямой правильной треугольной призмы без срезов, а затем выполнить на ее фронтальной проекции срезы плоскостями частного положения по заданному условию: фронтально-проецирующей плоскостью 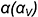 и профильной плоскостью
и профильной плоскостью 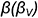 .
.
2-е действие. Обозначить на фронтальной проекции призмы характерные точки пересечения плоскостей срезов с ребрами, гранями и основанием призмы:
-точки 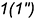 и
и 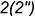 -лежат на ребрах призмы
-лежат на ребрах призмы 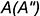 и
и 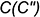 ;
;
-совпадающие точки 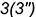 и
и 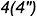 — лежат на гранях призмы и определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскостей срезов
— лежат на гранях призмы и определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскостей срезов 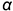 и
и 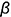 ;
;
- совпадающие точки
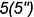 и
и 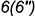 — лежат на верхнем основании призмы и определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскости
— лежат на верхнем основании призмы и определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскости 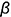 с верхним основанием призмы.
с верхним основанием призмы.
3-е действие. Достроить горизонтальную проекцию призмы со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек, и определить видимость плоскостей срезов:
3.1. Плоскость среза 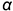 определяет четырехугольник
определяет четырехугольник 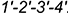 :
:
- точка
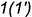 лежит на ребре
лежит на ребре 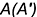 ;
; - точка
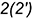 лежит на ребре
лежит на ребре 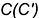 ;
; - совпадающие точки
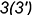 и
и 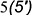 лежат на передней грани
лежат на передней грани 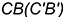 ;
; - совпадающие точки
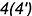 и
и 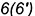 лежат на задней грани
лежат на задней грани 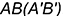 .
.
Четырехугольник 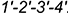 — искаженная по величине видимая горизонтальная проекция фронтально-проецирующей плоскости среза
— искаженная по величине видимая горизонтальная проекция фронтально-проецирующей плоскости среза 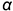 .
.
3.2. Плоскость среза 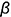 определяет совпадающие проекции отрезков
определяет совпадающие проекции отрезков 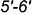 и
и 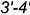 :
:
-отрезок 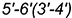 — горизонтальная, вырожденная в линию, видимая проекция профильной плоскости среза
— горизонтальная, вырожденная в линию, видимая проекция профильной плоскости среза 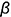 (проекция прямоугольника).
(проекция прямоугольника).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции призмы для определения ее очерка и внутреннего контура:
4.1. Горизонтальный очерк определяет треугольник 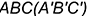 .
.
4.2. Внутренний контур определяет видимый отрезок 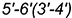 .
.
5-е действие. Достроить профильную проекцию призмы, построив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов:
5.1. Плоскость среза 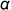 определяет видимый и искаженный по величине четырехугольник
определяет видимый и искаженный по величине четырехугольник 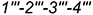 :
:
-точка 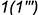 — лежит на ребре
— лежит на ребре 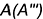
- точка
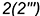 — лежит на ребре
— лежит на ребре 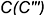 ;
; - точка
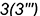 — построена по координате
— построена по координате 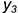 ;
;
-точка 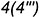 — лежит на задней грани
— лежит на задней грани 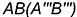 , которая спроецировалась в прямую.
, которая спроецировалась в прямую.
5.2. Плоскость среза 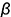 определяет видимая натуральная проекция прямоугольника
определяет видимая натуральная проекция прямоугольника 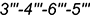 :
:
-точки 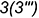 и
и 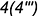 — уже построены, так как линия пересечения плоскостей среза 3-4 принадлежит плоскости
— уже построены, так как линия пересечения плоскостей среза 3-4 принадлежит плоскости 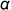 и плоскости
и плоскости 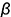 ;
;
- точка
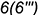 — лежит на задней грани
— лежит на задней грани 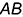
- точка
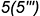 — построена по координате
— построена по координате 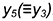 .
.
6-е действие. Выполнить графический анализ построенной профильной проекции призмы для определения ее очерка и внутреннего контура.
6.1. Профильный очерк определяют:
- слева — профильная проекция ребра
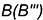 , совпадающая с проекцией грани
, совпадающая с проекцией грани 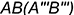
- справа — участок
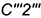 ребра
ребра 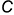 и ломаная линия
и ломаная линия 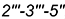
- снизу — отрезок
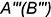 —
— 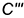 нижнего основания призмы;
нижнего основания призмы; - сверху — отрезок
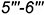 — линия пересечения плоскости
— линия пересечения плоскости 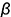 с верхним основанием призмы (участок основания).
с верхним основанием призмы (участок основания).
6.2. Внутренний контур определяют видимые отрезки 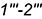 и
и 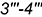 .
.
7-е действие. Оформить чертеж призмы, обведя сплошными толстыми линиями очерки и видимые линии внутреннего контура каждой ее проекции (оставить на чертеже тонкими сплошными линиями очерки проекции призмы без срезов и линии построения).
Построение проекций пирамиды со срезами плоскостями частного положения
На рис. 7.4 показан пример построения проекций правильной треугольной пирамиды со срезами, выполненными плоскостями частного положения: фронтально-проецирующей плоскостью 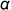 и профильной плоскостью
и профильной плоскостью 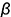 . Для упрощения графических описаний взята пирамида без срезов из предыдущего примера (см. рис. 7.2), фронтальная, горизонтальная и профильная проекции которой уже построены.
. Для упрощения графических описаний взята пирамида без срезов из предыдущего примера (см. рис. 7.2), фронтальная, горизонтальная и профильная проекции которой уже построены.
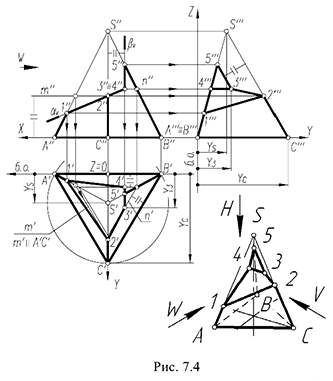
Для построения проекций пирамиды со срезами следует выполнить предлагаемый графический алгоритм, определяющий порядок действий при решении всех подобных задач.
1-е действие. Построить тонкими линиями на поле чертежа горизонтальную, фронтальную и профильную проекции заданной правильной треугольной пирамиды без срезов, а затем выполнить на ее фронтальной проекции срезы фронтально-проецирующей плоскостью 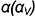 и профильной плоскостью
и профильной плоскостью 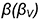 .
.
2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с ребрами и гранями пирамиды:
- точка
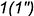 — на ребре
— на ребре 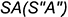 ;
; - точка
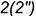 — на ребре
— на ребре 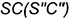 ;
;
-совпадающие точки 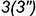 и
и 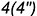 — на гранях
— на гранях 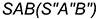 и
и 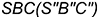 определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскостей срезов
определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскостей срезов 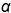 и
и 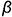 ;
;
- точка
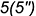 — на ребре
— на ребре 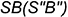 .
.
3-е действие. Достроить горизонтальную проекцию пирамиды со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек, и определить видимость плоскостей срезов.
3.1. Плоскость среза а определяет четырехугольник 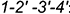 :
:
- точка
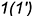 — на ребре
— на ребре 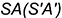 ;
;
-точка 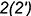 — на ребре
— на ребре 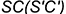 (построена на вспомогательной линии
(построена на вспомогательной линии 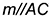 ), см. рис. 7.4);
), см. рис. 7.4);
- точки
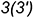 и
и 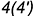 лежат на гранях пирамиды и построены с помощью вспомогательной линии
лежат на гранях пирамиды и построены с помощью вспомогательной линии 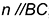 ;
;
-четырехугольник 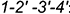 — горизонтальная, искаженная по величине видимая проекция фронтально-проецирующей плоскости
— горизонтальная, искаженная по величине видимая проекция фронтально-проецирующей плоскости 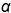 .
.
3.2. Плоскость среза 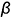 определяет отрезок
определяет отрезок 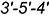 — вырожденная в видимую линию горизонтальная проекция профильной плоскости
— вырожденная в видимую линию горизонтальная проекция профильной плоскости 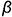 :
:
- точка
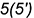 — на ребре
— на ребре 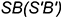 ;
; - точки
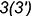 и
и 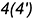 — построены.
— построены.
4-е действие. Выполнить графический анализ построенной горизонтальной проекции пирамиды со срезами для определения ее очерка и внутреннего контура.
4.1. Горизонтальный очерк определяет треугольник 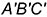 основания пирамиды.
основания пирамиды.
4.2. Внутренний контур определяют:
- видимый отрезок
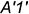 — участок ребра
— участок ребра  ;
; - видимый отрезок
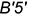 — участок ребра
— участок ребра  ;
; - видимый отрезок
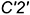 — участок ребра
— участок ребра 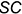 ;
; - видимый четырехугольник
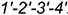 .
.
5-е действие. Достроить профильную проекцию пирамиды, построив проекции плоскостей срезов по профильным проекциям обозначенных точек и определить видимость плоскостей срезов.
5.1. Плоскость среза  определяет видимый четырехугольник
определяет видимый четырехугольник 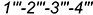
- точка
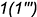 — лежит на ребре
— лежит на ребре 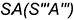
- точка
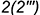 — лежит на ребре
— лежит на ребре 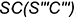 ;
; - точка
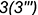 — построена по координате
— построена по координате 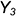 ;
;
-точка 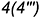 — лежит на задней грани
— лежит на задней грани 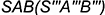 , вырожденной в линию;
, вырожденной в линию;
-четырехугольник 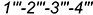 — искаженная по величине видимая проекция фронтально-проецирующей плоскостью
— искаженная по величине видимая проекция фронтально-проецирующей плоскостью  .
.
5.2. Плоскость среза 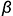 определяет видимая натуральная проекция треугольника
определяет видимая натуральная проекция треугольника 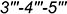 :
:
- точки
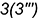 и
и 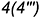 — уже построены (отрезок 3-4 — линия пересечения плоскостей среза
— уже построены (отрезок 3-4 — линия пересечения плоскостей среза 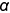 и
и 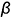 );
); - точка
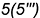 — лежит на ребре
— лежит на ребре 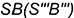 ;
; - отрезок
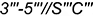 .
.
6-е действие. Выполнить графический анализ построенной профильной проекции пирамиды со срезами для определения ее очерка и внутреннего контура.
6.1. Профильный очерк определяют:
- слева — отрезок
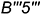 — участок ребра
— участок ребра  ;
;
-справа — отрезок 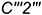 — участок ребра
— участок ребра 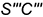 и ломаная линия
и ломаная линия 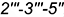 ;
;
- снизу — горизонтальная линия проекции основания
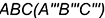 .
.
6.2. Внутренний контур определяют:
- видимый отрезок
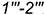 ;
; - видимый отрезок
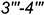 (линия пересечения плоскостей
(линия пересечения плоскостей  и
и 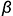 ).
).
7-е действие. Оформить чертеж пирамиды, выполнив сплошными толстыми линиями очерки и видимые линии внутреннего контура каждой ее проекции (тонкими линиями оставить на чертеже очерки проекции пирамиды без срезов и вспомогательные линии построения).
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Построение проекций правильной пирамиды |
| Построение проекций точек, лежащих на поверхности пирамиды |
| Поверхности вращения |
| Геометрические тела — цилиндр конус |

