Перпендикулярность
Решение задач на тему перпендикулярности прямой и плоскости основано на двух теоремах геометрии:
- 1-я теорема: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
- 2-я теорема: о проекции прямого угла (изложена выше — см. рис. 2.14, 2.15 и 2.16) — если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то на эту плоскость проекций угол проецируется прямым.
Из этих двух теорем следует, что на чертеже проекции перпендикуляра к плоскости можно провести только к проекциям фронтали и горизонтали, то есть к двум пересекающимся прямым уровня, которые можно провести в плоскости.
!!! Запомните:
- фронтальная проекция
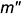прямой, перпендикулярной прямой к плоскости, перпендикулярна к фронтальной проекции 
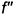фронтали этой плоскости 
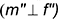; - горизонтальная проекция
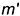прямой, перпендикулярной прямой к плоскости, перпендикулярна к горизонтальной проекции 
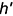горизонтали этой плоскости 
.
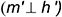Задачи на тему перпендикулярности прямой и плоскости можно разделить на три группы:
1-я группа. Провести от точки, лежащей в плоскости, перпендикуляр в пространство.
2-я группа. Провести из точки, не лежащей в плоскости, перпендикуляр к этой плоскости.
3-я группа. Построить плоскость, перпендикулярную к прямой общего положения (построить геометрическое место точек — ГМТ).
Первая группа задач требует по условию проведения перпендикуляра от плоскости (восставить перпендикуляр) в пространство (см. рис. 5.1).
В этой группе задач требуется, как правило, построить на проведенном перпендикуляре проекции отрезка заданной величины. Графические действия по построению проекций отрезка заданной величины на проекциях прямой общего положения изложены ранее (см. рис. 2.9).
На рисунке 5.1 показано решение примерной задачи первой группы: построить плоскость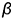 
, параллельную заданной плоскости 
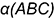, на расстоянии 
.
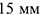Эта задача относится к первой группе, поскольку для построения параллельной плоскости 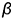нужно предварительно построить произвольную точку на расстоянии 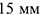от заданной плоскости 
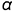, то есть из произвольной точки плоскости провести перпендикуляр в пространство.
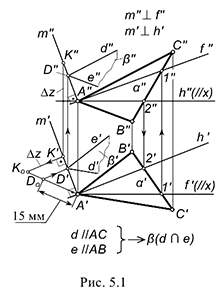
Для решения задачи требуется выполнить следующий графический алгоритм:
1-е действие. Провести в заданной плоскости общего положения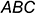 
проекции фронтали 
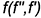и горизонтали 
:
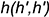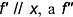— построить по вспомогательной точке 1;
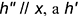— построить по вспомогательной точке 2.
2-е действие. Провести от точки плоскости, например, от вершины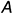 
в пространство проекции перпендикуляра 
:
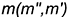- фронтальную проекцию
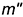перпендикулярно 
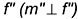; - горизонтальную проекцию
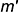перпендикулярно 
.
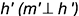3-е действие. На проекциях перпендикуляра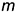 
построить проекции отрезка заданной величины 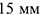, для чего выполнить следующие графические действия:
- Ограничить построенную прямую 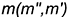произвольным отрезком
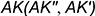. - Построить натуральную величину этого отрезка (см. рис. 5.1) способом прямоугольного треугольника — это гипотенуза
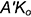. - На построенной гипотенузе отложить заданную величину
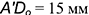и построить проекции отрезка 
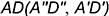заданной величины (см. построения), то есть проекции точки 
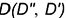, находящейся на расстоянии 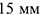от плоскости .
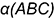4-е действие. Построить плоскость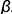 
, параллельную заданной плоскости 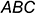, проведя через проекции точки 
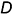две пересекающиеся прямые 
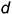и 
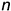, соответственно параллельные двум пересекающимся прямым 
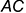и 
плоскости :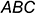
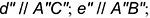
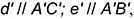то есть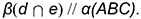 
Вторая группа задач требует по условию проведения перпендикуляра из точки в пространстве к плоскости (опустить перпендикуляр). В этой группе задач, как правило, требуется построить точку пересечения построенного перпендикуляра с заданной плоскостью.
Построение точки пересечения прямой общего положения с плоскостью общего положения было рассмотрено выше (см. рис. 4.6).
На рис. 5.2 показано решение примерной задачи второй группы: определить расстояние от точки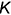 
до заданной плоскости 
.
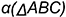Эта задача относится ко второй группе, так как расстояние от точки 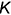до заданной плоскости 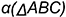определяется величиной перпендикуляра, проведенного из точки к плоскости.
Для решения задачи требуется выполнить следующий графический алгоритм:
1-е действие. Провести в плоскости фронталь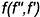 
и горизонталь 
.
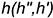2-е действие. Провести через заданную точку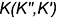 
проекции перпендикуляра 
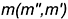к плоскости 
:
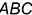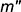перпендикулярно 
;
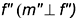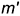перпендикулярно 
.
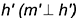3-е действие. Построить точку пересечения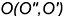 
перпендикуляра 
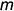с заданной плоскостью общего положения 
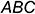, выполнив промежуточный графический алгоритм:
- Заключить прямую 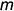во вспомогательную горизонтально-проецирующую плоскость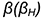
- Построить вспомогательную линию пересечения 3-4 заданной плоскости 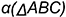со вспомогательной плоскостью
:
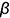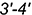— определяется на следе 
;
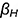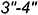— строится по принадлежности точек 3 и 4 сторонам 
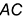и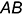 
треугольника ;
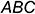- Определить проекции искомой точки пересечения 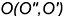на пересечении проекций построенной вспомогательной линии пересечения 3-4 с проекциями перпендикуляра .
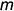4-е действие. Построить натуральную величину отрезка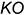 
способом прямоугольного треугольника, то есть определить расстояние от точки 
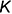до плоскости .
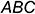Третья группа задач требует по условию построения некоторой вспомогательной плоскости (геометрического места точек), перпендикулярной к прямой общего положения. Эту перпендикулярную плоскость можно задать двумя пересекающимися прямыми, каждая из которых должна быть перпендикулярна прямой общего положения (теорема о перпендикулярности прямой и плоскости, т. е. признак перпендикулярности прямой и плоскости). На чертеже плоскость, перпендикулярную к прямой общего положения, можно задать только проекциями пересекающихся прямых уровня — фронтальной (параллельной плоскости проекций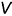 
) и горизонтальной (параллельной плоскости 
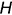), что соответствует теореме о проекции прямого угла. В задачах этой группы, как правило, требуется по условию определить точку пересечения заданной прямой со вспомогательной перпендикулярной плоскостью.
На рис. 5.3 показано решение примерной задачи третьей группы: определить расстояние от точки 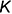до прямой общего положения .
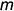Эта задача относится к третьей группе, поскольку на чертеже провести перпендикуляр к прямой общего положения, по которому определяется расстояние от точки 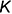до заданной прямой 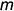, нельзя (прямой угол в этом случае не проецируется прямым). Следовательно, для решения нужно построить вспомогательную плоскость 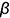, перпендикулярную к заданной прямой, которая будет геометрическим местом всех перпендикуляров к этой прямой.
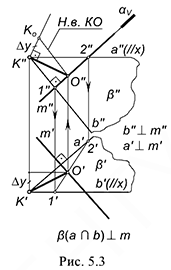
Для решения задачи требуется выполнить следующий графический алгоритм:
1-е действие. Построить троим вспомогательную плоскость 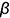, перпендикулярную заданной прямой 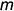, задав ее двумя пересекающимися прямыми уровня 
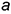и 
:
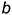- горизонтальной прямой
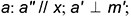
- фронтальной прямой
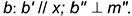
2-е действие. Построить точку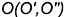 
пересечения заданной прямой 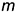со вспомогательной плоскостью 
по алгоритму построения точки пересечения прямой общего положения с плоскостью общего положения (см. рис. 5.3).
3-е действие. Соединить одноименные проекции точек 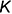и 
: полученный отрезок общего положения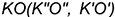
и есть расстояние от точки до прямой, искаженное на проекциях по величине.
4-е действие. Построить натуральную величину построенного отрезка 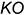способом прямоугольного треугольника (см. рис. 5.3).
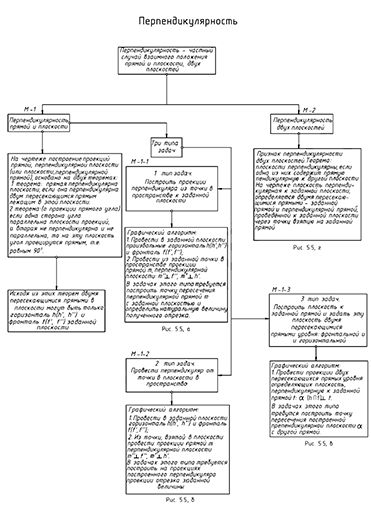
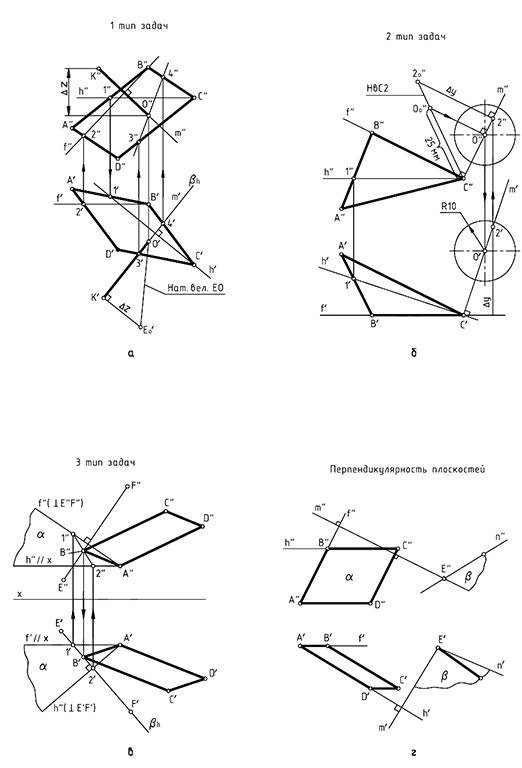
Структуризация материала пятой лекции в рассмотренном объеме схематически представлена на рис. 5.4 (лист 1). На последующем листе 2 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 5.5).
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Пересечение прямой с плоскостью |
| Взаимное положение двух плоскостей, прямой линии и плоскости |
| Плоскопараллельное перемещение |
| Способ замены (перемены) плоскостей проекций |
