Точка и прямая в плоскости

Точка и прямая в плоскости

Из геометрии известны теоремы о принадлежности точки и прямой линии плоскости:

1-я теорема: точка принадлежит плоскости, если она принадлежит прямой линии, лежащей в этой плоскости.

2-я теорема: прямая линия принадлежит плоскости, если она проходит через две точки, лежащие в этой плоскости.

На рис. 3.2 показано применение этих теорем для построения горизонтальной проекции точки 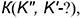лежащей в плоскости, заданной треугольником 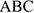. Для решения этой задачи требуется выполнить следующий графический алгоритм (графические действия):

1-е действие. Провести в заданной плоскости фронтальную проекцию вспомогательной прямой 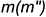через две точки этой плоскости — например, через точку 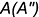и заданную фронтальную проекцию точки 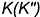; эта прямая пересекает сторону 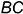треугольника в точке .

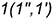2-е действие. Провести горизонтальную проекцию вспомогательной прямой 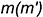через горизонтальные проекции точек 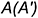и .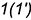

3-е действие. Построить по линии связи искомую горизонтальную проекцию точки 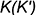на горизонтальной проекции вспомогательной прямой .

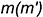На рис. 3.3, а, б показано решение задачи, где требуется достроить горизонтальную проекцию четырехугольника 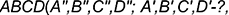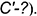Для решения задачи выполнены следующие графические построения:

• проведены проекции диагонали
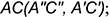
• проведена фронтальная проекция диагонали

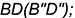
-определены проекции вспомогательной точки 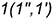, принадлежащей диагоналям 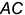и

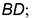
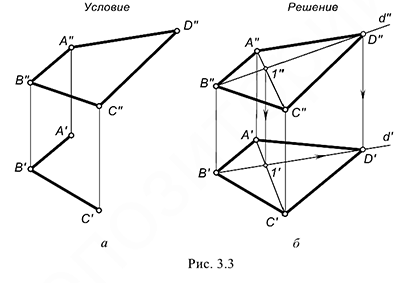
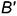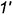-проведена через точки и горизонтальная проекция диагонали 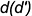, на которой должна лежать проекция вершины ;

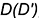• построена по линии связи горизонтальная проекция 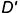вершины 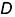по ее принадлежности прямой ;

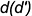-достроена горизонтальная проекция 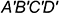четырехугольника .

Прямые особого положения в плоскости. Горизонталь 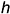и фронталь 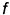плоскости

Прямые линии, лежащие в плоскости и параллельные фронтальной плоскости проекций , называются фронталями — .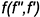

Прямые линии, лежащие в плоскости и параллельные горизонтальной плоскости проекций 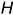, называются горизонталями — .

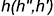На рис. 3.4 показано построение в плоскости треугольника проекций фронтали и горизонтали.

Поскольку фронталь плоскости 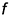параллельна фронтальной плоскости проекций 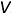, построение ее проекций следует начинать

с горизонтальной проекции фронтали 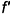которая должна быть на чертеже параллельна оси 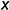. Фронтальная проекция фронтали 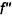строится по ее принадлежности заданной плоскости с помощью вспомогательной точки .

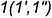Поскольку горизонталь плоскости 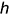параллельна горизонтальной плоскости проекций 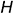, построение ее проекций следует начинать с фронтальной проекции горизонтали 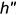которая должна быть на чертеже параллельна оси 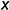. Горизонтальная проекция горизонтали 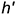строится по ее принадлежности заданной плоскости с помощью вспомогательной точки .

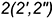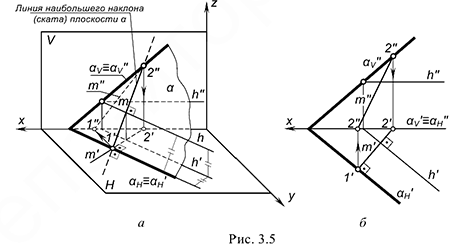
Прямые линии, лежащие в плоскости и перпендикулярные горизонтали этой плоскости, называются линиями наибольшего наклона (ската) плоскости. Они определяют угол наклона плоскости к плоскости проекций .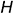

На рис. 3.5, а изображена линия наибольшего ската 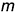в плоскости 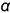, а на рис. 3.5, б — построение ее проекций на чертеже этой плоскости, заданной следами.

Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:

 Начертательная геометрия для 1 курса

Возможно эти страницы вам будут полезны:

Проекции плоскости

Взаимное положение двух прямых

Взаимное положение двух плоскостей, прямой линии и плоскости

Понятие о следах плоскости