Проекции прямой. Положение прямой относительно плоскостей проекций. Взаимное положение прямых. Способ прямоугольного треугольника. Теорема о проекции прямого угла
Прямая. Прямые общего и частных положений относительно плоскостей проекций. Определение натуральной величины отрезка общего положения. Понятие о следах прямой.
Относительно плоскостей проекций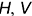 
и 
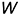прямые линии могут занимать различные положения и имеют соответствующие наименования, а на чертежах проекции этих прямых занимают относительно осей проекци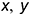й 
и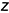 
характерные положения. Следовательно, по чертежу прямой линии можно мысленно представить ее пространственное положение относительно плоскостей проекций, т. е. научиться «читать» чертеж прямой.
Прямые общего положения — не параллельны (и соответственно не перпендикулярны) плоскостям проекци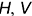й и 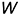. Следовательно, на чертеже проекции прямых общего положения не параллельны (и не перпендикулярны) осям проекци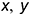й и 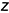. Отсюда проекции прямых общего положения искажают их натуральную величину.
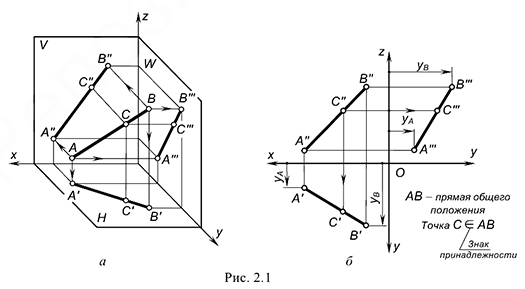
На рис. 2.1 изображены проекции прямой общего положения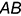 
, фронтальная 
и горизонтальная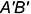 
проекции которой расположены произвольно относительно оси проекций 
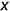, но не параллельны и не перпендикулярны оси 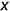— это характерный признак прямой общего положения на чертеже! Профильная проекция 
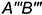прямой общего положения также должна быть не параллельна и не перпендикулярна осям проекци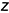й и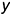 
, что и показывает построение.
Точка на прямой. Теорема о принадлежности точки прямой: если точка принадлежит прямой, то на чертеже одноименные проекции точки лежат на одноименных проекциях прямой. На рис. 1.4 показано построение проекций точки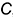 
, принадлежащей прямой 
.
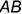Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Метод проекций. Образование чертежа по Монжу. Проекции точки |
| Касательные плоскости и нормаль к поверхности |
| Прямые особого (частного) положения |
| Понятие о следах прямой |
