Задача №142.
В трансмиссии, показанной на рис. 8.14, входное коническое колесо 1 в данный момент имеет угловую скорость 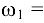
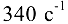 и постоянное угловое ускорение
и постоянное угловое ускорение 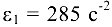 , направленное по движению.
, направленное по движению.
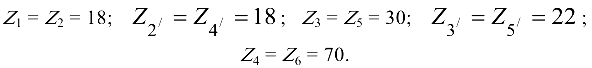
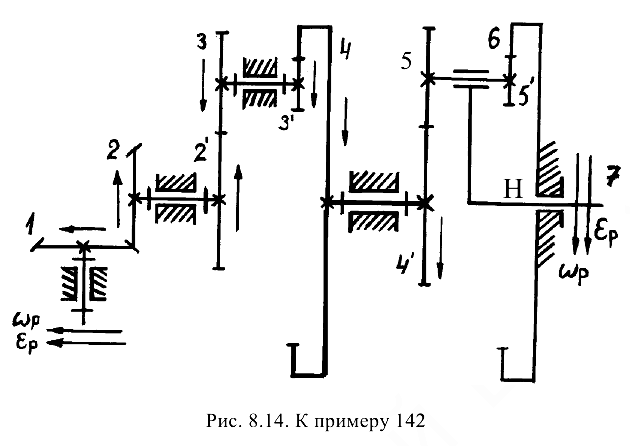
Припять средний модуль конического колеса 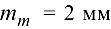 , ширину колеса
, ширину колеса 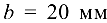 , плотность
, плотность 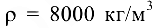 смещение центра масс (точки
смещение центра масс (точки 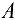 , рис. 8.15)
, рис. 8.15) 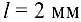 .
.
Определить:
1) передаточное отношение между входным и выходным звеньями и направление вращения;
2) угловую скорость и угловое ускорение выходного звена, их направление показать на схеме передачи;
3) время, в течение которого угловая скорость увеличится в 2 раза;
4) величину и направление силы инерции и моменты пары сил инерции звена 1 в начале и в конце найденного в предшествующем пункте промежутка времени, сравнить силу инерции с силой тяжести и показать на чертеже направление вращения, ускорения и инерционных нагрузок;
5) общий коэффициент полезного действия передачи.
Решение:
1. Определим передаточное отношение механизма:
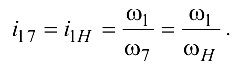
Выделим из механизма ступень с неподвижными осями, состоящую из колес
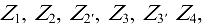
и планетарную ступень, состоящую из колес
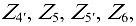
водила 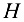 (7); а) для ступени с неподвижными осями
(7); а) для ступени с неподвижными осями
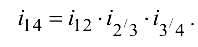
Оси колес 1 и 4 непараллельные, поэтому знак передаточного отношения не определяем, а покажем направления вращения колес неподвижной ступени в соответствии с правилом стрелок:
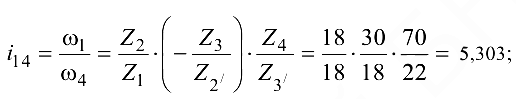
б) чтобы определить передаточное отношение планетарной ступени, используем формулу Виллиса; остановим водило 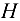 (7); используя зависимость (8.5), получим
(7); используя зависимость (8.5), получим
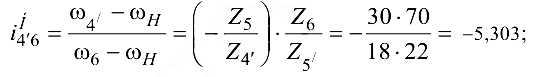
колесо 6 неподвижно (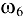 = 0), используя зависимость (8.6), получим
= 0), используя зависимость (8.6), получим
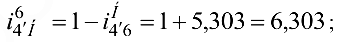
в) передаточное отношение всего механизма
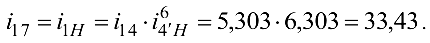
Передаточное отношение планетарной ступени 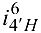 >0. Следовательно, водило
>0. Следовательно, водило 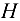 (7) вращается в ту же сторону, что и колесо 4′.
(7) вращается в ту же сторону, что и колесо 4′.
Покажем направление угловой скорости 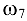 и углового ускорения
и углового ускорения 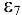 на чертеже стрелками.
на чертеже стрелками.
Поскольку 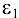 > 0, то вращение ускоренное.
> 0, то вращение ускоренное.
- Угловая скорость и угловое ускорение ведомого звена 7 по модулю
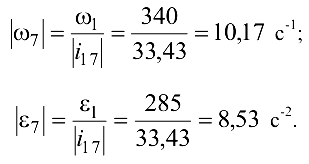
- Определить время, в течение которого угловая скорость увеличится вдвое:
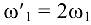 .
.
Для ускоренного вращения 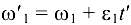 . Отсюда
. Отсюда
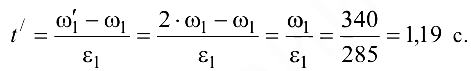
- Для расчета момента инерции
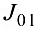 коническое ведущее колесо со средним модулем
коническое ведущее колесо со средним модулем 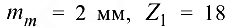 заменим цилиндром с диаметром, равным среднему делительному диаметру:
заменим цилиндром с диаметром, равным среднему делительному диаметру:
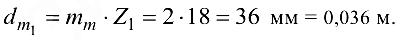
С учетом сказанного масса определяется по формуле
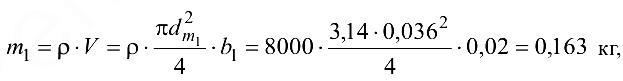
где 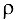 — плотность;
— плотность; 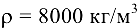 (по условию).
(по условию).
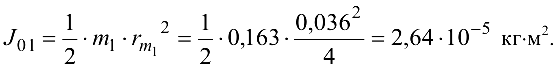
Вес колеса
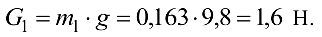
Смещение центра масс (точки 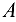 ) (рис. 8.15)
) (рис. 8.15) 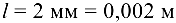 .
.
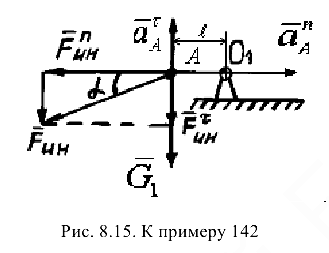
Нормальная составляющая силы инерции
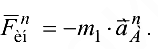
Нормальное ускорение точки 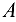
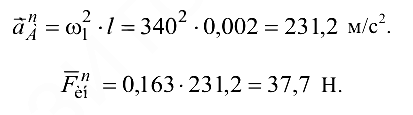
Касательное ускорение точки 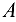 и касательная составляющая силы инерции
и касательная составляющая силы инерции
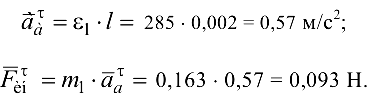
Определяем полное ускорение точки 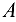 , силу инерции и направление силы инерции:
, силу инерции и направление силы инерции:
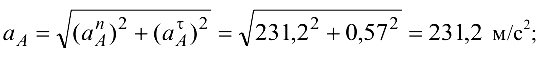
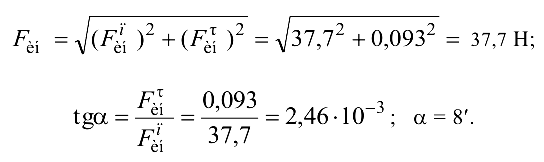
В практических расчетах составляющей 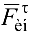 , как малой величиной, можно пренебречь и считать, что
, как малой величиной, можно пренебречь и считать, что
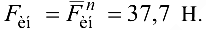
Сравним силу тяжести и силу инерции:
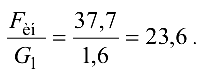
Силой веса по сравнению с силой инерции при практических расчетах также можно пренебречь. Момент сил инерции
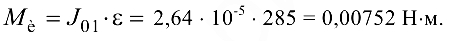
Покажем направление всех векторных величин па чертеже (см. рис. 8.15).
- Определим общий КПД механизма:
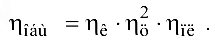
Здесь 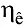 = 0,95 — КПД конической пары с учетом потерь в подшипниках;
= 0,95 — КПД конической пары с учетом потерь в подшипниках;
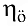 = 0,97 — КПД цилиндрической пары (2 пары по условию);
= 0,97 — КПД цилиндрической пары (2 пары по условию); 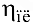 = 0,96 — КПД планетарной передачи.
= 0,96 — КПД планетарной передачи.
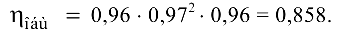
Ответ:
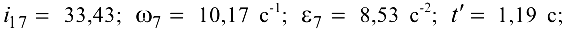
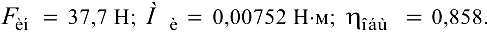
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

