Задача №84.
Однородная балка закреплена в точке 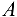 с помощью шарнирно-неподвижной опоры и поддерживается
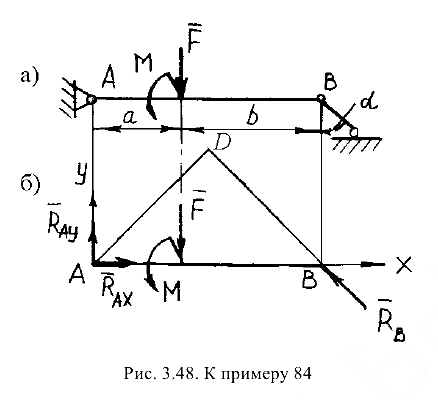
с помощью шарнирно-неподвижной опоры и поддерживается 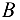 точке в стержнем (рис. 3.48, а). Найти реакции шарнирно-неподвижной опоры и стержня
точке в стержнем (рис. 3.48, а). Найти реакции шарнирно-неподвижной опоры и стержня 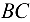 . Силой тяжести балки и стержня пренебречь.
. Силой тяжести балки и стержня пренебречь.
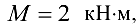
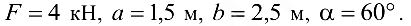
Решение:
Изобразим балку вместе с нагрузками, соблюдая заданные размеры ее участков и угла 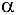 (рис. 3.48, б).
(рис. 3.48, б).
Освободим балку от связей в точках 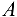 и
и 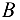 , заменив эти связи их реакциями. Начало координат поместим в точке
, заменив эти связи их реакциями. Начало координат поместим в точке 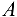 , ось
, ось 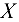 совместим с осью балки, а ось
совместим с осью балки, а ось 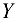 направим перпендикулярно балке. Если стержень растягивается, то его реакция направлена в сторону от рассматриваемого тела, а при сжатии — от стержня к телу. Составим три уравнения равновесия:
направим перпендикулярно балке. Если стержень растягивается, то его реакция направлена в сторону от рассматриваемого тела, а при сжатии — от стержня к телу. Составим три уравнения равновесия:
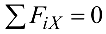 — алгебраическая сумма проекций сил на ось
— алгебраическая сумма проекций сил на ось 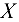 ;
;
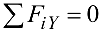 — алгебраическая сумма проекций сил на ось
— алгебраическая сумма проекций сил на ось 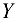 ;
;
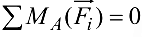 — алгебраическая сумма моментов относительно точки
— алгебраическая сумма моментов относительно точки 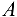 .
.
Уравнение проекций сил на ось 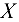 имеет вид
имеет вид
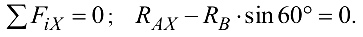
Силы 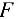 и
и 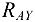 не вошли в уравнение, так как они перпендикулярны оси
не вошли в уравнение, так как они перпендикулярны оси 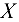 и их проекции на эту ось равны нулю. Проекции силы на ось
и их проекции на эту ось равны нулю. Проекции силы на ось 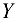
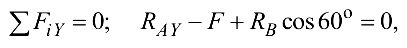
реакция 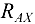 перпендикулярна оси
перпендикулярна оси 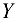 , и ее проекция на эту ось равна нулю.
, и ее проекция на эту ось равна нулю.
Для составления уравнения моментов за центр моментов принимаем точку 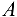 . Плечо силы
. Плечо силы 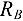 равно длине перпендикуляра, восстановленного из точки
равно длине перпендикуляра, восстановленного из точки 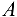 (центра моментов) к линии действия силы
(центра моментов) к линии действия силы 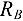 . Из рис. 3.48, б видно, что
. Из рис. 3.48, б видно, что
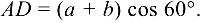
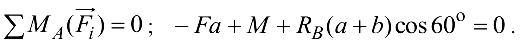
Подставив числовые значения, получим
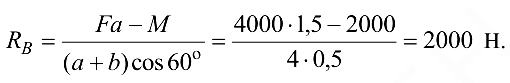
Выразим из (3.20)
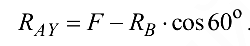
Подставив значения сил, получим
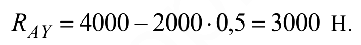
Из (3.19)
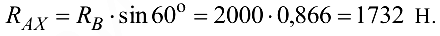
Проверим правильность решения задачи, составив уравнения моментов относительно точки 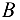 :
:
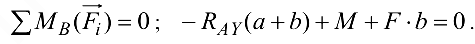
Подставим числовые значения:
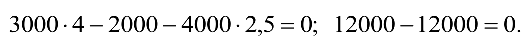
Задача решена верно, так как при подстановке получили тождество 0 = 0.
Полная реакция опоры 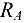
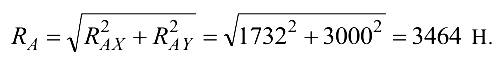
Ответ:
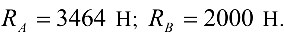
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

