Задача №74 с решением
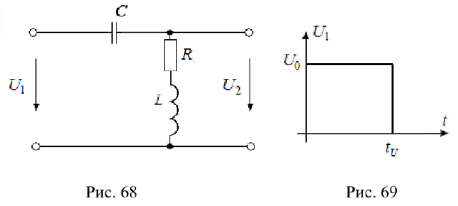
На вход цепи (рис. 68) с параметрами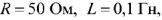 
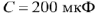подастся напряжение 
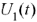в виде прямоугольного импульса (рис. 69) с амплитудой 
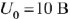и длительностью 
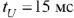. Найти напряжение
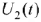с помощью интеграла Дюамеля и построить график.
Для определения напряжения 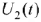необходимо определить переходную характеристику.
Для этого рассчитывается 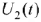при условии, что на входе подключается источник ЭДС 
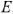, равный 1 В, т. е. схема примет вид, как показано на рис. 70.
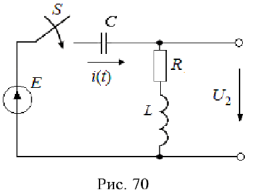
Напряжение 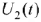можно определить, если известен переходный ток 
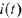в сопротивлении 
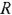и 
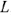, тогда 
.
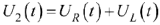Классическим методом переходный ток 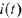определяется из условия, что
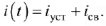
Ток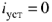 
, т. к. в цепи имеется конденсатор 
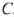, который не пропускает постоянный ток, тогда 
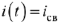. Вид свободной составляющей зависит от вида и количества корней характеристического уравнения.
Корни уравнения определяются из уравнения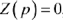 
, т. е. входное сопротивление цепи
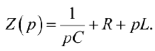
Решение квадратного уравнения имеет два действительных корня:
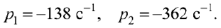
Следовательно:
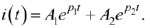
Ток в индуктивности в первый момент после коммутации равен току до коммутации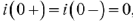 
, т. к. 
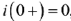, что следует из закона коммутации. Уравнение для определения постоянных интегрирования при 
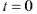имеет вид
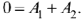
Второе уравнение можно получить, дифференцируя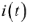 
и умножая на коэффициент 
:
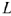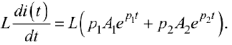
Выражение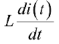 
представляет собой напряжение 
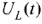на индуктивности. Определяя значение 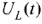для момента времени 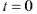, получаем второе уравнение для определения постоянных интегрирования:
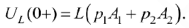
Напряжение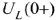 
— это зависимое начальное условие, которое определяется из уравнения, записанного по второму закону Кирхгофа для момента времени :
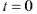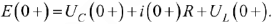
Так как согласно закону коммутаци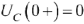и 
и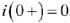 
, следовательно, 
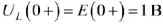. Система уравнений для определения 
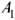и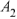 
имеет вид
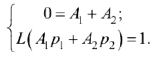
Откуда следует, что
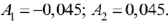
Так как
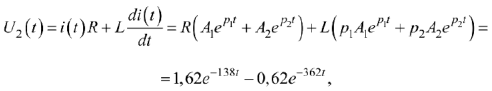
следовательно,
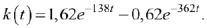
Интеграл Дюамеля для интервала времени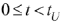 
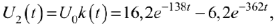
а на интервале времени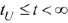 
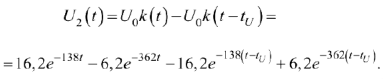
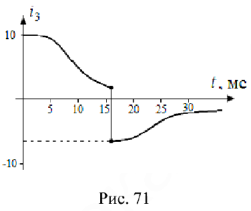
График переходного процесса изображен на рис. 71.
Эта задача взята со страницы решения задач по электротехнике:
Решение задач по электротехнике
Возможно эти задачи вам будут полезны:
| Задача №65 с решением |
| Задача №73 с решением |
| Задача №76 с решением |
| Задача №77 с решением |
