Задача №73 с решением
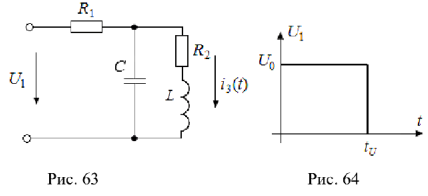
На вход цепи (рис. 63) с параметрами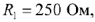 
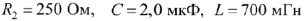подаётся напряжение 
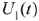в виде прямоугольною импульса (рис. 64) с амплитудой 
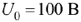и длительностью 
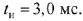Найти ток индуктивности 
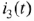с помощью интеграла Дюамеля и построить график.
Для расчёта с помощью интеграла Дюамеля определяется переходная проводимость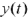 
, которая равна значению переходного тока 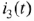исходной схемы при условии, что на входе подключается постоянный источник ЭДС, равный 1 В. Переходную проводимость рассчитываем классическим методом.
Корни характеристического уравнения определяются из условия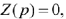 
т.е.
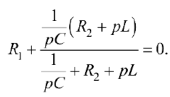
После подстановки исходных значений уравнение имеет вид
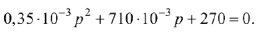
Корни уравнения:
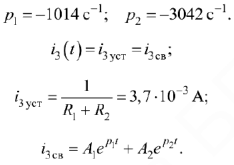
Так как до коммутации ток в индуктивности был равен нулю, то но закону коммутации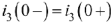 
,следовательно, уравнение для определения постоянных интегрирования 
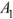и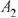 
имеет вид
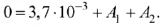
Второе уравнение определяется путём дифференцирования и умножения на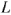 
выражения :
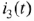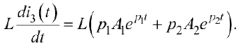
Выражение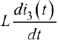 
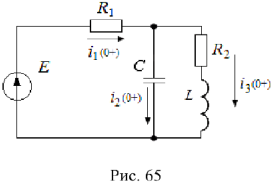
представляет собой напряжение на индуктивности. Значение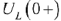 
— это зависимое начальное условие, которое в общем случае определяется из системы уравнений, записанных по законам Кирхгофа для исходной схемы (рис. 65) для момента времени 
.
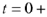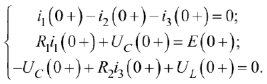
Так как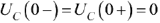 
и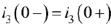 
,то из третьего уравнения следует, что 
.
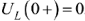Постоянные интегрирования 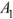и 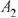определяются из системы
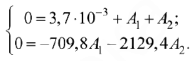
Следовательно: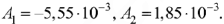 
Переходная проводимость
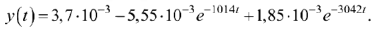
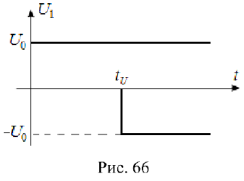
Импульс входного напряжения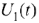 
можно рассматривать как сумму двух прямоугольных напряжений с одинаковой амплитудой, сдвинутых на интервал времени 
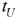(рис. 66).
Тогда на интервале времени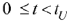 
интеграл Дюамеля будет
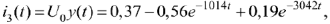
а на интеграле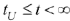 
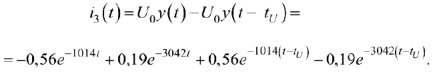
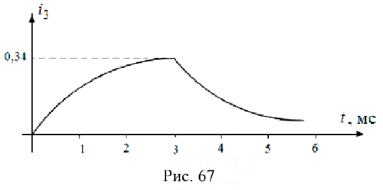
График переходного процесса проведен на рис. 67.
Эта задача взята со страницы решения задач по электротехнике:
Решение задач по электротехнике
Возможно эти задачи вам будут полезны:
| Задача №64 с решением |
| Задача №65 с решением |
| Задача №74 с решением |
| Задача №76 с решением |
