В соответствии с методом контурных токов, ток в любой ветви 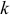 записывается в виде (3.111) или применяя понятия входные
записывается в виде (3.111) или применяя понятия входные 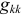 и взаимные
и взаимные 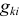 проводимости ветвей в виде уравнения:
проводимости ветвей в виде уравнения:
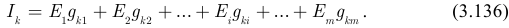
Если в схеме изменяется только одна ЭДС, например ЭДС 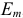 то все слагаемые в (3.136), кроме слагаемого
то все слагаемые в (3.136), кроме слагаемого 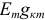 постоянны и могут быть для сокращения записи заменены постоянной величиной
постоянны и могут быть для сокращения записи заменены постоянной величиной 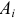 :
:

Для ветви 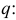

Решаем уравнение (3.138) относительно 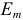 получим:
получим:

и подставляем 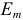 в уравнение (3.137) получим:
в уравнение (3.137) получим:
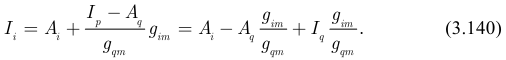
Вводим обозначения:
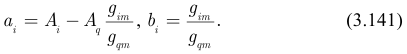
Следовательно:

Равенство (3.142) свидетельствует о том, что при изменении ЭДС 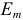 токи
токи 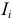 и
и 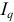 связаны линейной зависимостью. В соответствии с теоремой компенсации известно, что любое сопротивление можно заменить ЭДС. Следовательно, изменение сопротивления в
связаны линейной зависимостью. В соответствии с теоремой компенсации известно, что любое сопротивление можно заменить ЭДС. Следовательно, изменение сопротивления в 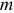 ветви эквивалентно изменению ЭДС
ветви эквивалентно изменению ЭДС 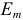 . Следовательно, линейное соотношение (3.142) выполняется и при изменении только одного сопротивления в схеме. Если обе части равенства (3.142) умножить на сопротивление
. Следовательно, линейное соотношение (3.142) выполняется и при изменении только одного сопротивления в схеме. Если обе части равенства (3.142) умножить на сопротивление 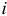 -ой ветви
-ой ветви 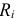 получим:
получим:
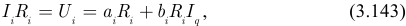

где
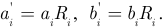
Следовательно, напряжение 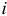 -ой ветви линейно связано с током
-ой ветви линейно связано с током 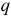 ветви.
ветви.
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:
