Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью
Если в неразветвлённой цепи с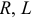 
и 
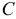(рис. 9.12 а) протекает синусоидальный ток 
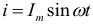, то он создает падение напряжения на всех участках цепи:
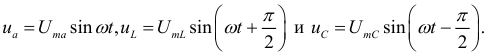
Мгновенное значение напряжения дети определяется по формуле:
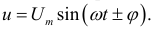
Так как в рассматриваемой цепи включены два реактивных сопротивления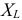 
и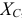 
, то возможны три режима работы цепи: 
.
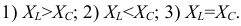Векторная диаграмма цепы для режима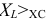 
изображена на рисунке 9.11 б.
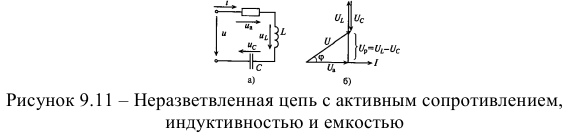
Знак перед углом сдвига фаз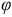 
зависит от режима работы цепи. Если в рассматриваемой цепи преобладает индуктивное напряжение (сопротивление), т. е. 
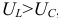, то цепь имеет индуктивный характер и напряжение 
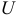опережает по фазе ток 
.
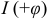Если в цепи преобладает ёмкостное напряжение (сопротивление), т. е.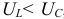 
, то цепь имеет ёмкостной характер и напряжение 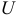отстаёт по фазе от тока 
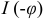. Из векторной диаграммы (рис. 3.166) следует:
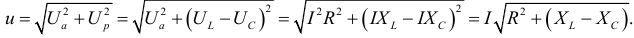
Сопротивление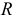 
может включать в себя сопротивление самостоятельного резистора или активное сопротивление реальной катушки и конденсатора.
Математическое выражение закона Ома для неразветвленной цепи с активным сопротивлением, индуктивностью и емкость:
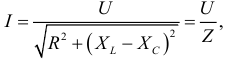
где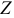 
— полное сопротивление неразветвленной цепи с 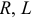и 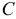, т. е.
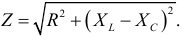
На рисунке 9.12 изображены векторная диаграмма напряжений, треугольники сопротивлений и мощностей для рассматриваемой цепи.
Знак и значение угла 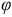можно определить из треугольника сопротивлений (рис. 9.12 6):
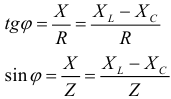
Из треугольника мощностей (рис. 9.12 в) видно, что в цепи с 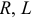и 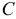кроме активной мощности 
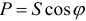имеется реактивная мощность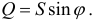 
Из треугольника мощностей (рис. 9.12 в) видно, что реактивная мощность, которая загружает источник и провода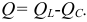 
Полная мощность цепи определяется по формуле: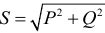 
Эта страница взята со страницы лекций по предмету теоретические основы электротехники (ТОЭ):
Предмет теоретические основы электротехники
Возможно эти страницы вам будут полезны:
