Правило Лопиталя
Некоторые свойства производных оказываются полезны при сравнении бесконечно больших и бесконечно малых величин.
Правило Лопиталя в случае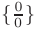 
. Пусть функции 
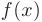и 
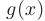непрерывны и дифференцируемы в окрестности точки 
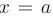и обращаются в нуль в самой точке: 
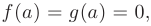причем 
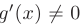в окрестности этой точки. Тогда, если существует предел отношения
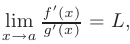
то будет верно равенство:
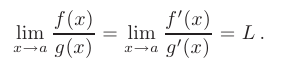
Правило Лопиталя в случае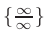 
. Пусть функци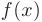и и 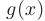непрерывны и дифференцируемы в окрестности точки 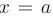кроме, может быть, самой точки и неограниченно возрастают в ее окрестности:
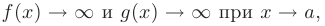
причем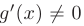 
в окрестности точки а. Тогда, если существует предел отношения
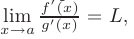
то будет верно равенство:
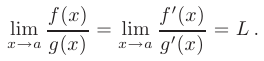
Заметим, что неопределенности вида
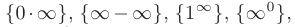
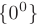
сводятся к неопределенностям вида 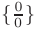или 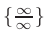с помощью тождественных преобразований:
- Пусть известны пределы двух функций:
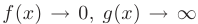при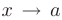 
. Тогда предел произведения этих функций может быть записан в виде:
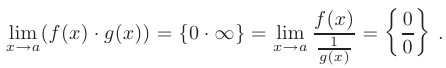
Пусть известны пределы двух функци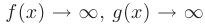й: 
при 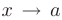. Тогда предел разности этих функций может быть записан в виде:
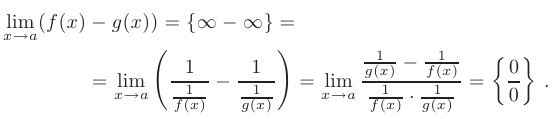
Пусть известны пределы двух функций:
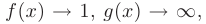
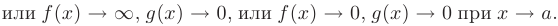
Тогда для нахождения предела показательно-степенной функции от этих функций следует воспользоваться основным логарифмическим тождеством:
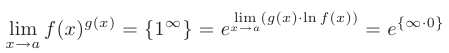
или
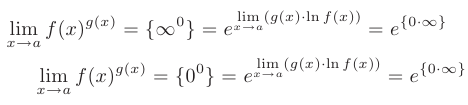
Далее, неопределенность вида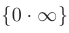 
раскрывается по схеме, показанной в пункте 1.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Производные и дифференциалы высших порядков в математике |
| Теоремы о дифференцируемых функциях в математике |
| Возрастание и убывание функции в математике |
| Максимум и минимум функции в математике |
