Производные и дифференциалы высших порядков
Производная функции 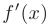 сама по себе является функцией независимой переменной
сама по себе является функцией независимой переменной 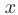 и называется производной первого порядка. Если полученная функция
и называется производной первого порядка. Если полученная функция 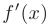 дифференцируема, то ее производная
дифференцируема, то ее производная
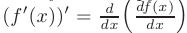
называется производной второго порядка и обозначается как:
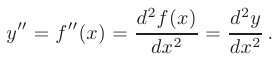
Производной третьего порядка называется производная от производной второго порядка, если последняя существует и дифференцируема:
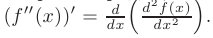
Записывается производная третьего порядка в виде
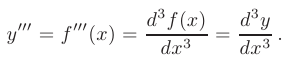
Аналогично, производной 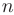 -го порядка называется производная от производной (
-го порядка называется производная от производной (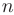 — 1)-го порядка, если последняя существует и дифференцируема:
— 1)-го порядка, если последняя существует и дифференцируема:
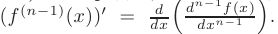
Все производные выше третьего порядка обычно обозначаются в виде верхнего индекса арабскими цифрами в круглых скобках. Так производные четвертого и  -го порядка могут быть записаны в виде:
-го порядка могут быть записаны в виде:
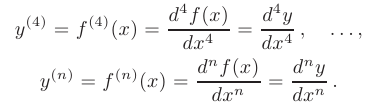
Так как дифференциал функции 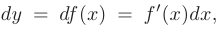 называемый также дифференциалом первого порядка, также является функцией независимой переменной
называемый также дифференциалом первого порядка, также является функцией независимой переменной 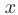 , то дифференцируя ее повторно можно получить выражения для дифференциалов второго, третьего и более высоких порядков:
, то дифференцируя ее повторно можно получить выражения для дифференциалов второго, третьего и более высоких порядков:
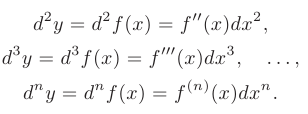
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Производные основных элементарных функций в математике |
| Дифференциал функции в математике |
| Теоремы о дифференцируемых функциях в математике |
| Правило Лопиталя в математике |

