Оглавление:
Приемы раскрытия неопределенностей. Первый и второй замечательные пределы
- При вычислении пределов выражений с тригонометрическими функциями удобно использовать первый замечательный предел и его следствие:
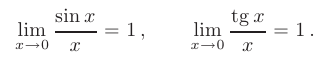
- При вычислении пределов выражений с показательно-степенными функциями также используется второй замечательный предел в различных формах:
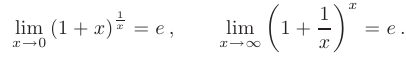
Предел отношения многочленов в бесконечно удаленной точке
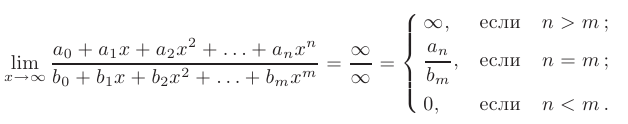
Пример:
Требуется найти указанные пределы:
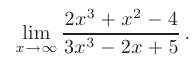
► В данном пределе при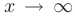 
числитель и знаменатель дроби многочлены неограниченно возрастают, т.е. мы сталкиваемся с неопределенностью вида
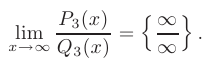
Освобождение от неопределенности такого вида возможно с помощью формулы предела отношения многочленов.
В нашем случае старшие степени числителя и знаменателя дроби совпадают:
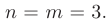
Следовательно, работает вторая строка формулы, по которой предел отношения многочленов равен отношению коэффициентов при старших степенях:
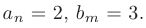
Отсюда раскрываем неопределенность:
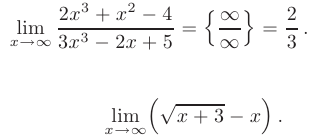
► В данном пределе при 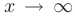оба слагаемых неограниченно возрастают, т.е. мы сталкиваемся с неопределенностью вида
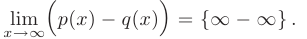
Освобождение от неопределенности такого вида возможно путем умножения выражения на сопряженное с использованием формулы разности квадратов. В нашем случае исходное выражение следует умножить на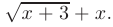 
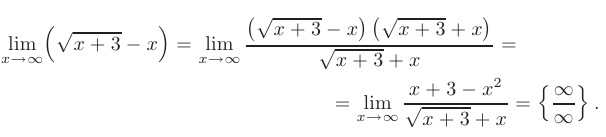
Проведенные преобразования приводят нас к новой неопределенности вида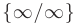 
. Поделим числитель и знаменатель дроби на старшую из степеней 
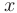, т.е. на 
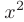. Используя свойства пределов, получим предел заданного выражения:
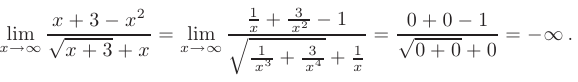
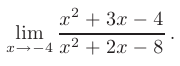
► В данном пределе при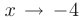 
числитель и знаменатель дроби стремятся к нулю. т.е. мы сталкиваемся с неопределенностью вида
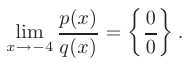
Для освобождения от неопределенности такого вида разложим числитель и знаменатель на множители по формуле:
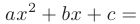
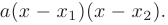
Учитывая, что и числитель и знаменатель дроби обращаются в нуль при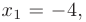 
второй корень каждого трехчлена можно определить с помощью следствия из теоремы Виета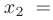 
В таком случае числитель и знаменатель могут быть записаны как:
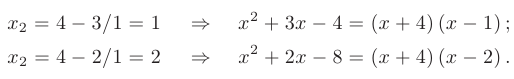
Тогда предел исходного выражения будет равен
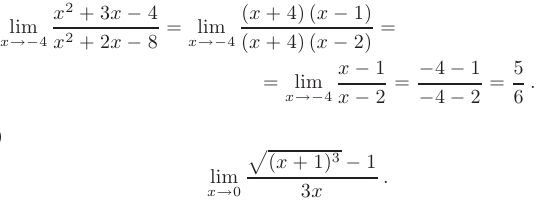
► В данном пределе при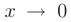 
числитель и знаменатель дроби стремятся к нулю, т.е. мы сталкиваемся с неопределенностью вида
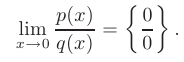
Для освобождения от неопределенности такого вида вначале избавимся от иррациональности. Для этого выполним замену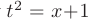 
или 
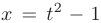. Заметим, что условие предельного перехода изменится с 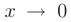на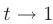 
:
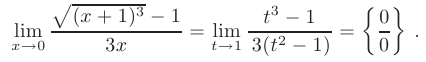
Теперь разложим числитель и знаменатель на множители и найдем предел искомого выражения:
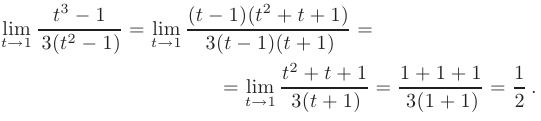
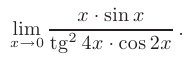
► В данном пределе при 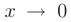числитель и знаменатель дроби стремятся к нулю. т.е. мы сталкиваемся с неопределенностью вида
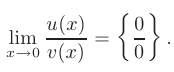
Освободиться от неопределенности такого вида можно с помощью первого замечательного предела и/или его очевидного следствия:
Таким образом, для решения нашего примера необходимо разложить заданную дробь на ряд множителей вышеуказанного вида: функция (синус или тангенс), деленная на аргумент функции:
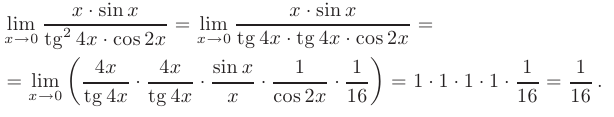
Заметим, что функции вида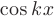 
в данном случае играют роль константы, так как предел 
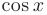при 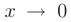равен единице.
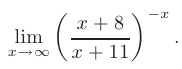
► Вначале выделим целую часть дроби, находящейся в основании показательно-степенной функции:
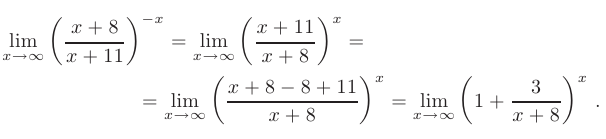
В данном пределе при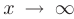 
основание показательно-степенной функции (в скобках) стремится к единице, а ее показатель — к бесконечности, т.е. мы сталкиваемся с неопределенностью вида
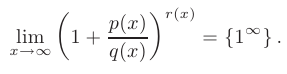
Освободиться от неопределенности такого вида можно с помощью второго замечательного предела:
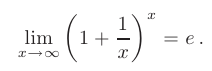
Выполним замену переменной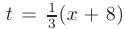 
или 
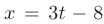. Заметим, что условие предельного перехода 
при этом не изменится. После этого преобразуем полученное выражение и найдем искомый предел:
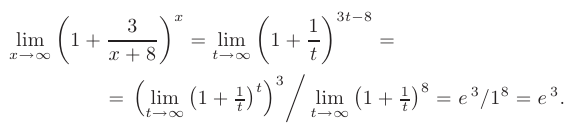
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Предел функции в математике |
| Бесконечно малые и бесконечно большие функции в математике |
| Непрерывность функции в математике |
| Асимптоты графика функции в математике |
