Предел функции
Пусть функция 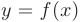 определена в некоторой окрестности точки
определена в некоторой окрестности точки 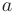 , кроме быть может самой точки
, кроме быть может самой точки 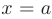 .
.
Определение предела функции. Число 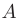 называется пределом функции
называется пределом функции 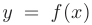 в точке
в точке 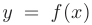 при
при 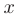 стремящимся к
стремящимся к 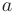 , если для любого положительного числа
, если для любого положительного числа 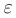 найдется такое положительное число
найдется такое положительное число 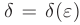 , что для всех
, что для всех 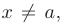 , удовлетворяющих неравенству
, удовлетворяющих неравенству 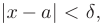 , выполняется неравенство
, выполняется неравенство 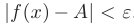 . Геометрическая интерпретация определения предела функции в точке
. Геометрическая интерпретация определения предела функции в точке 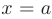 состоит в том, что для всех
состоит в том, что для всех 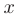 , достаточно близких к а значение функции
, достаточно близких к а значение функции 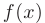 как угодно мало отличаются от числа
как угодно мало отличаются от числа 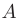 .
.
В более компактной форме факт существования предела функции в точке можно записать так:
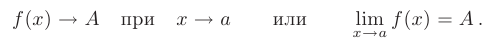
Свойства пределов функций. Будем считать, что пределы функций
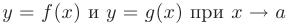
существуют. Тогда выполняются следующие свойства:
- Предел суммы или разности двух функций равен сумме или разности их пределов:
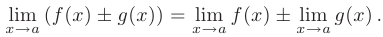
- Функция может иметь только один предел при
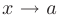 :
:
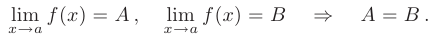
- Предел произведения двух функций равен произведению их пределов:
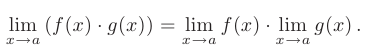
- Постоянный множитель можно выносить за знак предела:
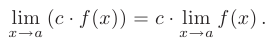
- Предел степени с натуральным показателем равен той же степени предела:
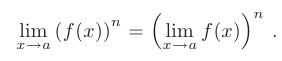
- Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю:
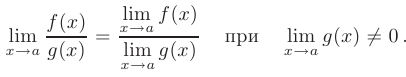
- Если в окрестности точки
 значения первой функции меньше значений второй, то и предел первой функции не превосходит предела второй при
значения первой функции меньше значений второй, то и предел первой функции не превосходит предела второй при  :
:
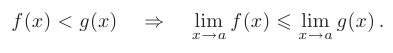
- Если
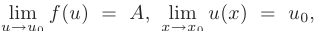
- то и предел сложной функции
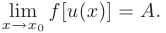
Если функция 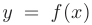 определена на промежутке
определена на промежутке 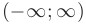 , то число
, то число 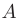 называется пределом функции
называется пределом функции 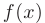 при
при 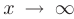 , если для любого положительного числа
, если для любого положительного числа 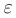 найдется такое положительное число
найдется такое положительное число 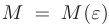 , что для всех
, что для всех 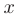 , удовлетворяющих неравенству
, удовлетворяющих неравенству 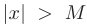 , выполняется неравенство
, выполняется неравенство 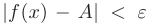 . В более компактной форме факт существования предела функции при
. В более компактной форме факт существования предела функции при 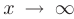 можно записать так:
можно записать так:
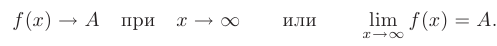
Число 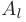 называется пределом функции
называется пределом функции 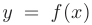 слева в точке
слева в точке 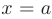 , если для любого положительного числа
, если для любого положительного числа 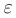 найдется такое положительное число
найдется такое положительное число 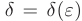 , что при
, что при 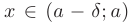 выполняется неравенство
выполняется неравенство 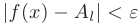 . В более компактной форме факт существования левостороннего предела функции в точке можно записать так:
. В более компактной форме факт существования левостороннего предела функции в точке можно записать так:
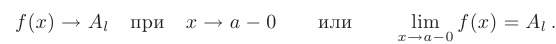
Число 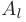 называется пределом функции
называется пределом функции 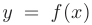 справа в точке
справа в точке 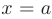 , если для любого положительного числа
, если для любого положительного числа 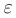 найдется такое положительное число
найдется такое положительное число 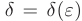 , что при
, что при 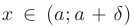 выполняется неравенство
выполняется неравенство 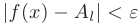 . В более компактной форме факт существования правостороннего предела функции в точке можно записать так:
. В более компактной форме факт существования правостороннего предела функции в точке можно записать так:
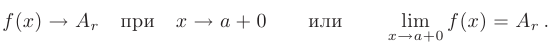
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Предел последовательности в математике |
| Функция одной переменной в математике |
| Бесконечно малые и бесконечно большие функции в математике |
| Раскрытие неопределённостей в математике |

