Эллипс
Эллипсом называется геометрическое место точек плоскости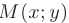 
, для которых сумма расстояний до двух фиксированных точек, называемых фокусами 
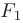и 
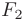, есть величина постоянная:
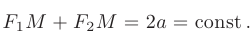
Если фокусы эллипса
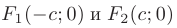
расположены на оси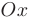 
симметрично относительно начала координат 
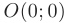(см. рис. 2.7), то уравнение эллипса имеет канонический вид
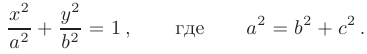
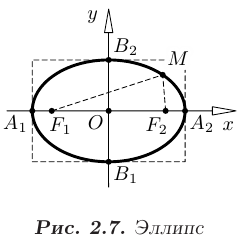
Точки с координатами:
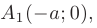
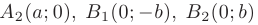
называют вершинами эллипса. Отрезок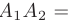 
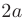образует большую ось, а отрезок 
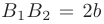— малую ось эллипса. Тогда величины 
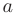и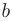 
будут равны соответственно большой и малой полуосям эллипса. Форма эллипса определяется отношением половины фокусного расстояния к большой полуоси — эксцентриситетом эллипса: 
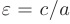, причем 
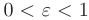, так как 
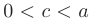. Если эксцентриситет эллипса принять равным нулю: 
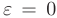, то полуоси эллипса 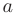и 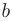будут равны друг другe и эллипс выродится в окружность
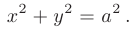
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Уравнения прямой и плоскости в пространстве в математике |
| Уравнения линий второго порядка на плоскости в математике |
| Гипербола в математике |
| Парабола в математике |
