Оглавление:
Уравнение прямой на плоскости
Уравнение прямой, проходящей через точку плоскости 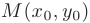 и имеющей нормальный вектор
и имеющей нормальный вектор 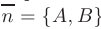 . записывается в виде
. записывается в виде
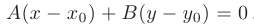
Используя обозначение
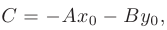
получим общее уравнение прямой на плоскости:
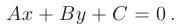
Две прямые, заданные своими общими уравнениями
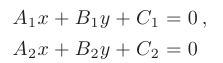
параллельны тогда и только тогда, когда соответствующие коэффициенты при переменных  и
и  пропорциональны, т.е.:
пропорциональны, т.е.:
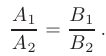
Две прямые, заданные своими общими уравнениями, перпендикулярны тогда и только тогда, когда верно равенство
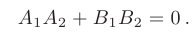
Уравнение прямой, проходящей через две точки плоскости 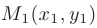 и
и 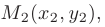 записывается в виде
записывается в виде
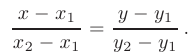
Тангенс угла наклона этой прямой к оси  называется угловым коэффициентом прямой:
называется угловым коэффициентом прямой:
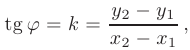
а ее направляющий вектор
имеет координаты, равные
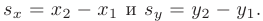
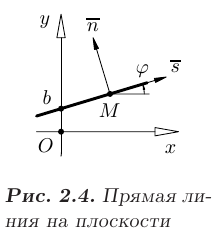
Уравнение прямой с известным угловым коэффициентом 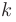 имеет вид
имеет вид
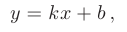
где 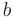 — величина отрезка, отсекаемого данной прямой на оси
— величина отрезка, отсекаемого данной прямой на оси 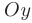 от начала координат,
от начала координат, 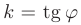 (см. рис. 2.4).
(см. рис. 2.4).
Объединив полученные результаты, запишем уравнение прямой с известным угловым коэффициентом 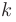 , проходящей через точку плоскости
, проходящей через точку плоскости 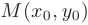 :
:
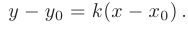
Под углом между прямыми на плоскости понимают наименьший из двух смежных углов, образованных этими прямыми. Если две прямые заданы уравнениями с угловыми коэффициентами:
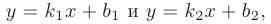
то угол 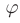 между ними определяется по формуле
между ними определяется по формуле
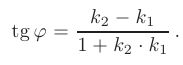
Условие параллельности этих прямых имеет вид
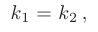
а условие перпендикулярности:
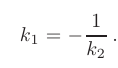
Расстоянием  от точки
от точки 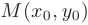 до прямой
до прямой 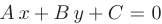 называется длина перпендикуляра, опущенного из этой точки на прямую. Расстояние
называется длина перпендикуляра, опущенного из этой точки на прямую. Расстояние 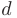 определяется по формуле
определяется по формуле
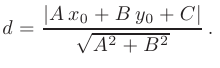
Пример:
Даны координаты вершин треугольника 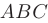 :
:
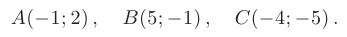
Требуется: 1) найти длину стороны 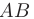 ; 2) составить уравнения сторон
; 2) составить уравнения сторон 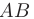 и
и 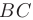 и вычислить их угловые коэффициенты; 3) вычислить внутренний угол при вершине
и вычислить их угловые коэффициенты; 3) вычислить внутренний угол при вершине 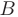 в радианах; 4) составить уравнение медианы
в радианах; 4) составить уравнение медианы 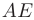 ; 5) составить уравнение и вычислить длину высоты
; 5) составить уравнение и вычислить длину высоты 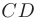 : 6) составить уравнение прямой, проходящей через точку
: 6) составить уравнение прямой, проходящей через точку 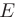 параллельно стороне
параллельно стороне 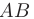 и определить координаты точки
и определить координаты точки 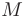 ее пересечения с высотой
ее пересечения с высотой 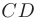 : 7) составить уравнение окружности с центром в точке
: 7) составить уравнение окружности с центром в точке 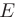 , проходящей через вершину
, проходящей через вершину 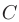 .
.
Указание. Заданный треугольник, все полученные линии и характерные точки необходимо построить в системе координат 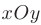 .
.
► 1. Найдем длину стороны 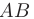 . Расстояние между двумя точками
. Расстояние между двумя точками
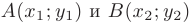
определяется по формуле
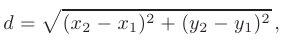
воспользовавшись которой находим длину стороны  :
:
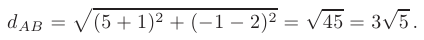
- Составим уравнения сторон
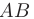 и
и 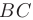 и вычислим их угловые коэффициенты. Уравнение прямой, проходящей через две заданные точки плоскости
и вычислим их угловые коэффициенты. Уравнение прямой, проходящей через две заданные точки плоскости
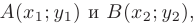
- имеет вид
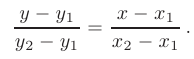
Подставляя в формулу координаты точек 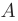 и
и 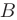 , получаем общее уравнение стороны
, получаем общее уравнение стороны 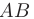 :
:
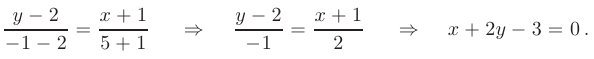
Угловой коэффициент 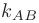 для прямой
для прямой 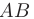 найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом
найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом 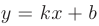 . В нашем случае:
. В нашем случае:
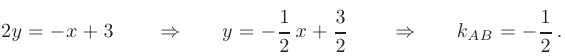
Аналогично получим общее уравнение прямой 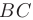 и найдем ее угловой коэффициент
и найдем ее угловой коэффициент 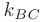 :
:
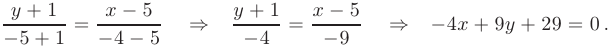
Далее:
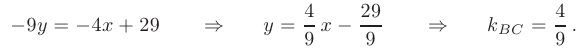
- При нахождении внутреннего угла
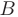 для заданного треугольника
для заданного треугольника 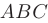 воспользуемся формулой
воспользуемся формулой
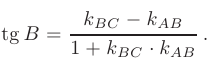
Подставив ранее вычисленные значения 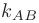 и
и 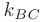 , находим:
, находим:
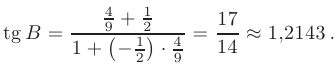
Теперь, воспользовавшись таблицами значений тригонометрических функций или инженерным микрокалькулятором, получаем значение угла в радианах 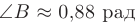 .
.
- Для составления уравнения медианы
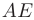 вычислим сначала координаты точки
вычислим сначала координаты точки 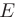 , которая лежит на середине отрезка
, которая лежит на середине отрезка 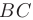 :
:
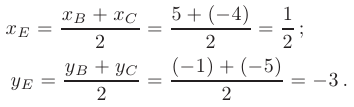
Подставив координаты точек 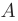 и
и 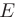 в уравнение прямой, проходящей через две заданные точки, получаем общее уравнение медианы
в уравнение прямой, проходящей через две заданные точки, получаем общее уравнение медианы 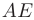 :
:
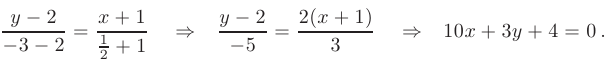
- Для составления уравнения высоты
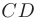 воспользуемся условием перпендикулярности прямых
воспользуемся условием перпендикулярности прямых 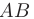 и
и 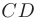 :
:
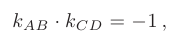
откуда следует, что
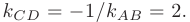
Подставив в уравнение
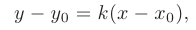
значение 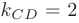 и соответствующие координаты точки
и соответствующие координаты точки  , найдем общее уравнение высоты
, найдем общее уравнение высоты  :
:
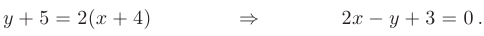
Длину высоты  определим как расстояние
определим как расстояние  от заданной точки
от заданной точки  (—4; 5) до прямой
(—4; 5) до прямой 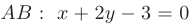 по формуле
по формуле
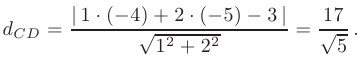
- Составим уравнение прямой, проходящей через точку
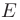 параллельно стороне
параллельно стороне 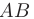 . Воспользуемся условием параллельности прямой
. Воспользуемся условием параллельности прямой 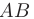 и искомой прямой
и искомой прямой 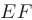 :
:
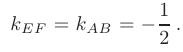
Подставив в уравнение
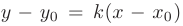
координаты точки 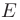 и значение
и значение 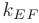 . получим искомое уравнение прямой
. получим искомое уравнение прямой 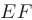 :
:

Координаты точки 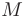 , как точки пересечения прямых
, как точки пересечения прямых 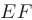 и
и 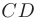 , найдем, объединив уравнения этих прямых в систему и решив ее:
, найдем, объединив уравнения этих прямых в систему и решив ее:

Отсюда координаты точки 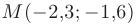 (см. рис. 2.5).
(см. рис. 2.5).
- Запишем уравнение окружности с центром в точке
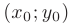 и радиусом, равным
и радиусом, равным 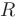 в каноническом виде
в каноническом виде
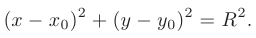
По условию радиус искомой окружности равен расстоянию от ее центра (точки 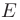 ) до точки
) до точки 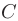 . В таком случае можно записать, что
. В таком случае можно записать, что 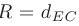 а следовательно и
а следовательно и 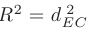 :
:
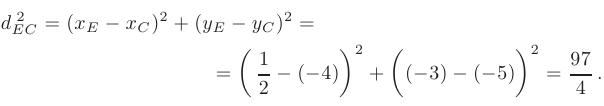
Заменив в уравнении окружности координаты центра 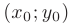 на координаты точки
на координаты точки 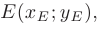 а
а 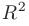 на
на 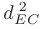 получим искомое уравнение окружности:
получим искомое уравнение окружности:
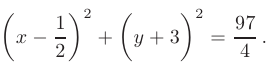
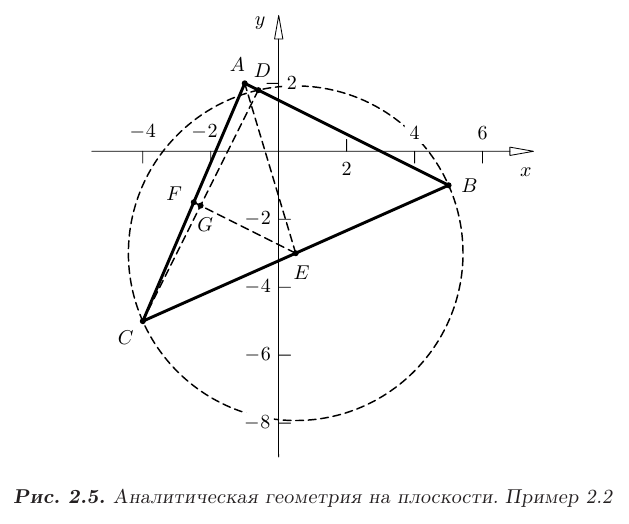
На рис. 2.5 показано построение заданного треугольника  , а также всех полученных линий и характерных точек в системе координат
, а также всех полученных линий и характерных точек в системе координат  .
.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:

