Приведем примеры разложения некоторых элементарных функций по формуле Маклорtна (2) предыдущего пункта.
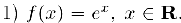
Для этой функции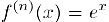 
при любом натуральном n и, значит,
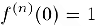. Поэтому
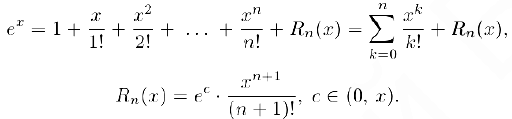
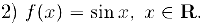
Здесь
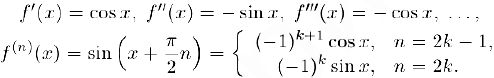
Поэтому,
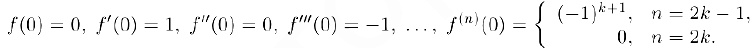
Следовательно, формула Маклорена порядка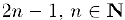 
для этой функции имеет вид:
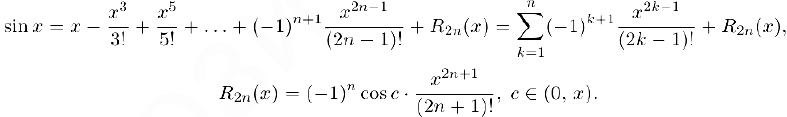
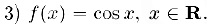
По аналогии с предыдущей функцией в этом случае при любом натуральном n
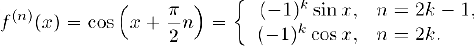
Следовательно,
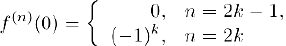
и, стало быть, формула Маклорена порядка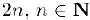 
для данной функции выглядит следующим образом:
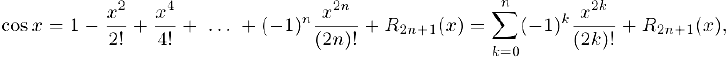
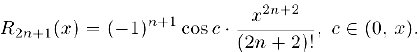
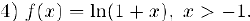
Производные этой функции равны:
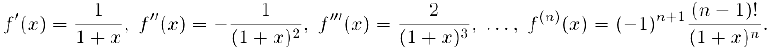
Значит,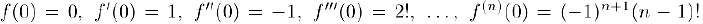 
и, стало быть,
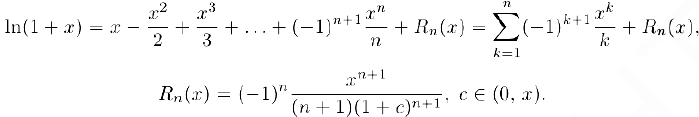
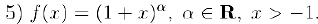
Для данной функции
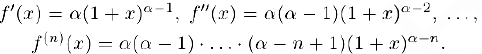
Отсюда
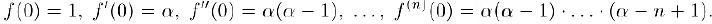
Запишем формул}’ Маклорена порядка п для этой функции:
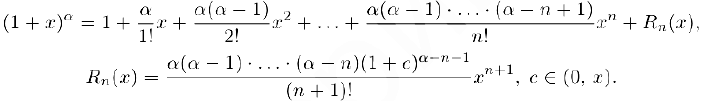
В частности, при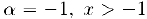 
получим:
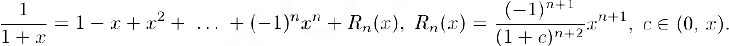
Замечание. Если мы можем записать функцию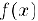 
в некотором интервале, содержащем точку 
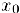. как алгебраическую сумму с действительными коэффициентами функций вида 
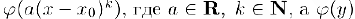, — одна из функций, рассмотренных в примерах 1) — 5). то. использовав разложения (1) — (5), мы получим представление функции 
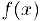по формуле Тейлора в точке 
.
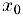Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
