Определение производной и дифференциала и их основные свойства
Рассмотрим функцию 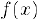 , определенную в некотором интервале, содержащем точку
, определенную в некотором интервале, содержащем точку 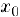 .
.
Определение 1. Если существует конечный предел
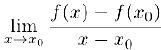
то он называется производной функции 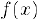 в точке .то и обозначается через
в точке .то и обозначается через 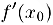 . Переформулируем определение производной на языке приращений. Пусть
. Переформулируем определение производной на языке приращений. Пусть
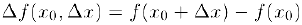
— приращение функции в точке 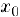 , соответствующее приращению аргумента
, соответствующее приращению аргумента 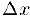 . Тогда приведенное выше определение производной равносильно существованию конечного предела
. Тогда приведенное выше определение производной равносильно существованию конечного предела
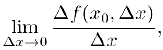
т. с. производная представляет собой предел отношения приращения функции в данной точке к приращению аргумента при условии, что приращение аргумента бесконечно мало.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:

