Оглавление:
Частные производные сложной функции
Предположим, что в формуле
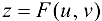
переменные 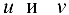 являются непрерывными функциями независимых переменных
являются непрерывными функциями независимых переменных 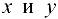 :
:
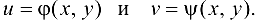
В этом случае функция 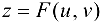 является сложной функцией аргументов
является сложной функцией аргументов 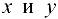 .
.
Предположим, что функции 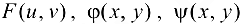 имеют непрерывные частные производные по всем своим аргументам. Вычислим частные производные
имеют непрерывные частные производные по всем своим аргументам. Вычислим частные производные 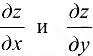 , исходя из формул (16.1) и (16.2) и не используя непосредственное представление функции z через
, исходя из формул (16.1) и (16.2) и не используя непосредственное представление функции z через 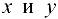 .
.
Придадим аргументу 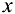 приращение
приращение 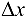 , сохраняя значение
, сохраняя значение 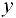 неизменным. Тогда, в силу (16.2),
неизменным. Тогда, в силу (16.2), 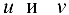 получат приращения
получат приращения 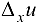 и
и 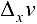 , но тогда и функция
, но тогда и функция 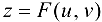 получит следующее приращение:
получит следующее приращение:
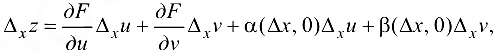
где 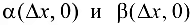 — бесконечно малые функции при
— бесконечно малые функции при 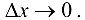 .
.
Разделим обе части формулы на 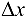 :
:
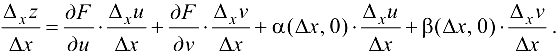
Если 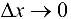 , то, в силу непрерывности
, то, в силу непрерывности 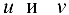 ,
, 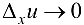 и
и 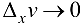 .
.
Переходя к пределу при 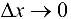 , получим
, получим
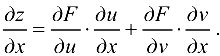
Если придать аргументу 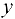 приращение
приращение 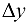 , сохраняя значение
, сохраняя значение 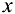 неизменным, то с помощью аналогичных рассуждений можно получить
неизменным, то с помощью аналогичных рассуждений можно получить
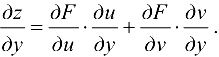
Пример 16.1.
Найти частные производные 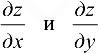 для функции
для функции 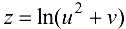 , если
, если 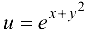 и
и 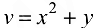 .
.
Решение:
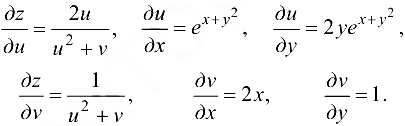
Получим
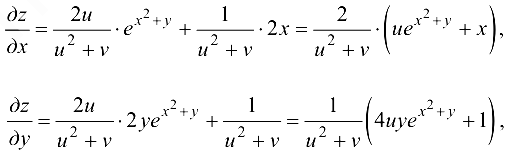
где 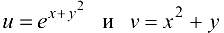 .
.
Заметим, что при записи ответа в выражения для частных производных вместо 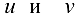 можно подставить их выражения через
можно подставить их выражения через 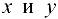 , однако это повлечет за собой громоздкие выражения.
, однако это повлечет за собой громоздкие выражения.
Ответ: 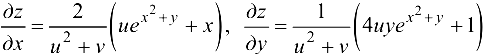 ‘
‘
где 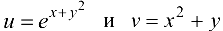 .
.
Для случая большего числа переменных формулы (16.3) и (16.4) естественным образом обобщаются. Например, если 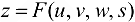 , где
, где 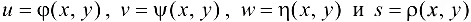 , то
, то
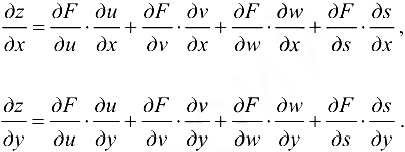
Пусть исходная функция имеет вид 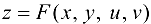 , где
, где 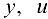 и
и 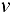 зависят от одной переменной
зависят от одной переменной 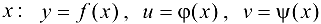 . Тогда, по сути, функция
. Тогда, по сути, функция 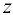 является функцией только одной переменной
является функцией только одной переменной 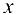 и можно ставить вопрос о нахождении производной
и можно ставить вопрос о нахождении производной 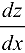 , которая называется полной производной функции
, которая называется полной производной функции 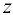 :
:
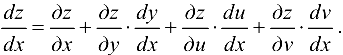
Пример 16.2.
Найти 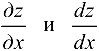 для функции
для функции 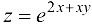 , если
, если 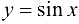 .
.
Решение:
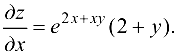
Формула (16.5) в данном случае принимает вид:
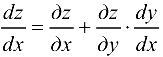
Поэтому
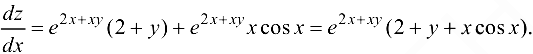
Ответ: 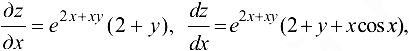 ,
,
где 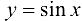 .
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

