Оглавление:
Дифференцируемость фнп
Определение 14.1. Функция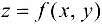 
называется дифференцируемой в точке 
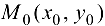, если ее полное приращение в этой точке можно представить в виде
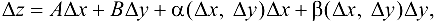
где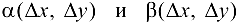 
— бесконечно малые функции при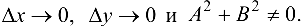 
Теорема 14.1. Если функция 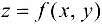дифференцируема в точке 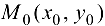, то она непрерывна в этой точке.
Доказательство.
Если функция 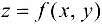дифференцируема в точке 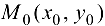, то из формулы (14.1) следует, что 
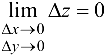или
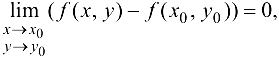
откуда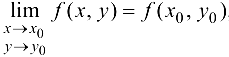 
, что и означает непрерывность функции в точке. ■
Теорема 14.2 (необходимые условия дифференцируемости).
Если функция 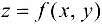дифференцируема в точке 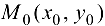, то она имеет в этой точке частные производные 
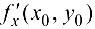и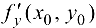 
причем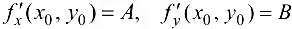 
Доказательство.
Так как функция 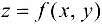дифференцируема в точке 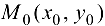, то ее приращение в этой точке представимо в виде (14.1). Полагая 
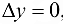, получим
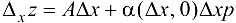
где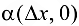 
— бесконечно малая функция при 
.
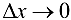Разделив полученное выражение на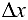 
и перейдя к пределу при 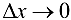, получим
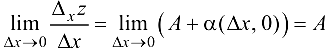
С другой стороны, по определению частной производной,
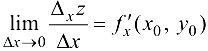
Следовательно, в точке 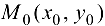существует 
.
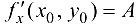Аналогично доказывается, что в точке 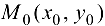существует 
.■
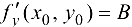Замечание 14.1. Обратные утверждения к теоремам 14.1 и 14.2 не верны, т. е. из непрерывности ФНП в точке 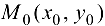и существования частных производных не следует дифференцируемость.
Пример 14.1.
Функция
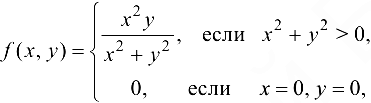
непрерывна на всей плоскости, на всей плоскости имеет частные производные, однако формула (14.1) не имеет места для данной функции в точке (0; 0).
Теорема 14.3* (достаточное условие дифференцируемости). Если функция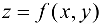 
имеет частные производные в некоторой 
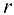-окрестности точки 
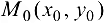, непрерывные в самой точке 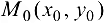, то функция дифференцируема в этой точке.
Понятие дифференцируемости для функции трех и более переменных вводится аналогично.
Определение 14.2. Функция нескольких переменных, дифференцируемая в каждой точке некоторого множества, называется дифференцируемой на этом множестве.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
