Оглавление:
Асимптоты графика функции
При исследовании поведения функции на бесконечности, т. е. при 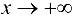 и при
и при 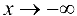 или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к некоторой прямой.
или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к некоторой прямой.
Определение 9.4. Прямая 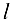 называется асимптотой графика функции
называется асимптотой графика функции 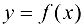 , если расстояние
, если расстояние 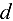 от переменной точки графика функции
от переменной точки графика функции 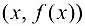 до прямой
до прямой 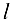 стремится к пулю при удалении точки
стремится к пулю при удалении точки 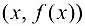 от начала системы координат.
от начала системы координат.
Существуют три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение 9.5. Прямая 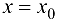 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 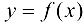 , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений 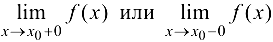 равно
равно 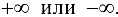 .
.
В этом случае расстояние от точки графика функции 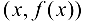 до прямой
до прямой 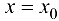 равно
равно 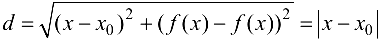 и, следовательно,
и, следовательно, 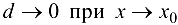 .
.
Пример 9.6.
График функции 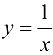 имеет вертикальную асимптоту
имеет вертикальную асимптоту 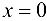 , так как
, так как 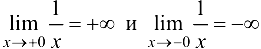 .
.
Определение 9.6. Прямая 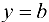 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 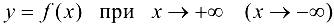 , если
, если 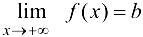 .
.
В этом случае расстояние от точки графика функции 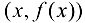 до прямой
до прямой 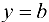 равно
равно 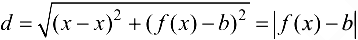 и, следовательно,
и, следовательно, 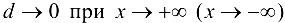 , так как
, так как 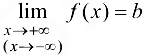 .
.
Пример 9.6 (продолжение).
График функции 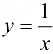 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 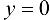 и при
и при 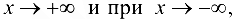 , так как
, так как 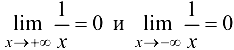 .
.
Определение 9.7. Прямая 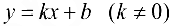 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 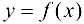 при
при 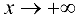
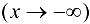 , если функцию
, если функцию 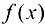 можно представить в виде
можно представить в виде
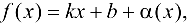
где 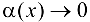 при
при 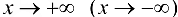 .
.
Теорема 9.7. Для того чтобы прямая 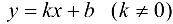 являлась наклонной асимптотой графика функции
являлась наклонной асимптотой графика функции 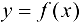 при
при 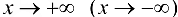 , необходимо и достаточно, чтобы существовали конечные пределы:
, необходимо и достаточно, чтобы существовали конечные пределы:
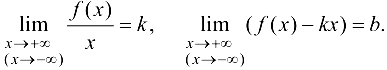
Доказательство. Рассмотрим случай 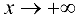 .
.
Необходимость.
Если 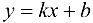 — наклонная асимптота графика функции
— наклонная асимптота графика функции 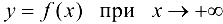 , то, используя представление функции по формуле (9.1), получим:
, то, используя представление функции по формуле (9.1), получим:
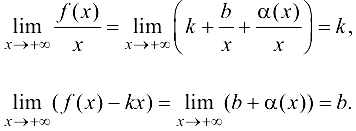
Достаточность.
Пусть существуют пределы (9.2). Тогда из второго равенства следует, что
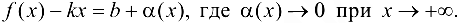
Полученное равенство легко преобразовать к виду (9.1), т. е. прямая 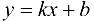 — наклонная асимптота графика функции
— наклонная асимптота графика функции 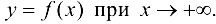 . ■
. ■
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

